1-2-2 ส่วนประกอบของเวกเตอร์ความเร็ว

จากสมการที่ 1-1 สำหรับเวกเตอร์บอกตำแหน่ง ซึ่งเราอาจจะแยกคิดเป็นแต่ละแกน หรือจะคิดแบบรวมๆ ก็ได้

จากนิยามของความเร็ว เราเขียนความเร็วของอนุภาคได้เป็น

(1-8)
(1-9)
หรือ
(1-10)

โดยสมการที่ (1-10) แสดงส่วนประกอบความเร็วของอนุภาคตามแนวแกนทั้งสาม ดังนั้นขนาดของความเร็ว หาได้จาก
(1-11)

บางครั้งเราจะเขียน แทน

ตัวอย่างที่ 1-1
 
        อนุภาคหนึ่งมีการเคลื่อนที่ตามสมการ เมื่อ x มีหน่วยเป็น m และ t มีหน่วยเป็น s จงหา
        (ก) ความเร็วเฉลี่ยของอนุภาคในช่วงเวลา 2s ถึง 3s


        (ข) ความเร็วของอนุภาคที่ t=2s และ t=3s


ตัวอย่างที่ 1-2
        
        จากกราฟแสดงตำแหน่งของอนุภาคซึ่งเคลื่อนที่ในหนึ่งมิติเทียบกับเวลา ดังรูป ต้องการทราบว่า ณ เวลาใดที่ความเร็วมีค่ามากกว่าศูนย์ น้อยกว่าศูนย์ และเป็นศูนย์

        วิธีทำ
        ความชันของเส้นสัมผัสของกราฟตำแหน่งเทียบกับเวลาที่เวลาต่างๆ ก็คือ ความเร็วขณะใดขณะหนึ่ง ณ เวลานั้นจะเห็นว่า
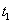
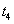
        ที่เวลา และ นั้นกราฟมีความชันเป็นศูนย์นั่นคือความเร็วมีค่าเป็นศูนย์
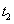
        ที่เวลา กราฟมีความชันเป็นลบนั่นคือความเร็วมีค่าน้อยกว่าศูนย์
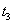
        ที่เวลา กราฟมีความชันเป็นบวกนั่นคือความเร็วมีค่ามากกว่าศูนย์