ในการบรรยายเรื่องการเคลื่อนที่ของวัตถุนั้น สิ่งแรกที่ต้องบอกได้คือ ต้องบอกได้ว่าวัตถุอยู่ที่ไหน ถ้าเป็นกรณีง่ายที่สุดคือ วัตถุมีการเคลื่อนที่ในหนึ่งมิติ ซึ่งก็คือการเคลื่อนที่ในแนวเดียว เช่น รถวิ่งไปตามถนนตรงที่ไม่มีทางแยกเลย หรือ มดเดินตามเส้นลวดตรง หรือ การปาวัตถุขึ้นในแนวดิ่งและตกลงมาในแนวเดิม หรือ การเข็นของขึ้นลงพื้นเอียง ตำแหน่งของวัตถุในการเคลื่อนที่เหล่านี้สามารถบรรยาย ได้ด้วยตัวแปรเพียงตัวเดียว โดยอาจจะเป็น x หรือ y หรือ θ ก็ได้ ความจริงแล้วการเคลื่อนที่ส่วนใหญ่ที่เรียนในตอนแรก จะเป็นการเคลื่อนที่ในหนึ่งมิติทั้งนั้น และเราก็จะบอกว่าที่เวลาต่างๆ นั้น ตัวแปร x มีค่าเป็นอย่างไร

ความเร็วเป็นปริมาณพื้นฐานอันหนึ่ง ที่ใช้บรรยายการเคลื่อนที่ของวัตถุ เกิดขึ้นเพราะมนุษย์ต้องการที่จะวัดการกระจัดต่อหน่วยเวลา นั่นคือต้องการที่จะบอกว่า วัตถุมีการเปลี่ยนแปลงตำแหน่งได้เร็วหรือช้าเพียงใด ในทางฟิสิกส์นั้น คำว่า ความเร็ว แตกต่างจาก อัตราเร็ว โดยที่ความเร็วเป็นปริมาณเวกเตอร์ ความเร็วมีทั้งขนาดและทิศทาง ในขณะที่อัตราเร็วเป็นปริมาณสเกลาร์

1-2-1 ความเร็วเฉลี่ยและความเร็วขณะใดขณะหนึ่ง

ความเร็วเฉลี่ยและความเร็วขณะใดขณะหนึ่ง (average and instantaneous velocity)

รูปที่ 1-1 แสดงการเคลื่อนที่ของอนุภาคจาก A ไปยังจุด B

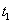
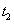
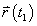
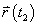
สมมติว่ามีอนุภาคอยู่ที่ตำแหน่ง A เมื่อเวลา จากนั้นอนุภาคเคลื่อนที่ไปยังตำแหน่ง B ตามแนวเส้นประ เมื่อเวลาผ่านไปเป็น โดยกำหนดให้ และ เป็นเวกเตอร์บอกตำแหน่ง ที่ลากจากจุดกำเนิด (origin) ซึ่งนับเป็นจุดอ้างอิงในกรณีนี้ ไปยังจุด A และ B ตามลำดับ

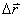
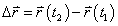
จากรูปที่ 1-1 จะพบว่าจาก A ไปยัง B อนุภาคมีการกระจัด ในช่วงเวลา Δt โดยที่ และ

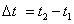
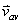
ดังนั้นความเร็วเฉลี่ย หรือ สามารถเขียนได้เป็น

(1-4)

หรือถ้าเป็นหนึ่งมิติก็จะเหลือเพียง

(1-5)

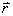
โดยที่ทั้ง x และ ต่างก็ขึ้นกับเวลา

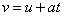
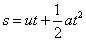
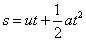
สมการที่ 1-5 เป็นสมการที่พบมากในระดับมัธยมปลาย หรือ การเรียนฟิสิกส์ในระยะแรก โดยเรียกกันว่า หรือ เช่นที่ปรากฏอยู่ในสูตร หรือ แต่นักเรียนมักจะคิดว่าตัวแปร นี้เป็นสเกลาร์ ทั้งที่ความจริงแล้ว เป็นเวกเตอร์จะถูกต้องมากกว่า และถ้านึกดีๆ เป็นบวกก็ได้ เป็นลบก็ได้ ซึ่งก็แสดงว่ามีทิศทาง และควรจะจำว่า ในสูตร นั้น เป็นการกระจัด ไม่ใช่ ระยะทาง

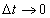
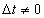
เนื่องจากความเร็วเฉลี่ย เป็นค่าตัวแทนของความเร็ว ตลอดการเคลื่อนที่ของอนุภาค ในช่วงเวลาที่สนใจ แต่ถ้าต้องการหาความเร็วขณะใดขณะหนึ่งเราก็สามารถหาได้เช่นกัน โดยพิจารณาการเคลื่อนที่ของอนุภาคในช่วงเวลาแคบๆ กล่าวคือ แต่ จากสมการที่ (1-1) ความเร็วขณะใดขณะหนึ่งหรือความเร็วขณะใดขณะหนึ่ง ณ ตำแหน่งใดๆ สามารถเขียนได้เป็น

(1-6)

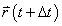
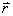
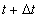
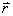
โดยที่ คือ ซึ่งเป็นฟังก์ชันของเวลา ที่เวลา และ คือ ที่เวลา t และสมการที่ 1-6 นี้ก็จะเทียบเคียงได้กับสมการ

(1-7)

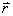
ที่พบในหนังสือ calculus ทั่วไป ดังนั้นถ้าพิจารณาสมการที่ (1-6) จะพบว่าความเร็วขณะใดขณะหนึ่งที่ตำแหน่งใดๆ ก็คือ อนุพันธ์ของ เทียบกับเวลานั่นเอง โดยมีทิศของความเร็วขณะใดขณะหนึ่งอยู่ในแนวเดียวกับเส้นสัมผัส ณ จุด A ที่เราสนใจ เช่นจากรูปที่ 1-1 ความเร็วขณะใดขณะหนึ่งที่จุด มีทิศทางตามแนวเส้นสัมผัสที่จุด A

หมายเหตุ ต่อไปถ้ากล่าวถึง "ความเร็ว" โดยไม่ได้ระบุรายละเอียดว่า เป็นความเร็วขณะใดขณะหนึ่งหรือ ความเร็วเฉลี่ย จะหมายถึง ความเร็วขณะใดขณะหนึ่งทั้งสิ้น