
ในหัวข้อที่ผ่านมา
เป็นการพิจารณาการเคลื่อนที่ของอนุภาค โดยเน้นเพียงใน
1 มิติ แต่ในความเป็นจริง การเคลื่อนที่ของวัตถุ อาจพิจารณาได้ใน
2 และ 3 มิติ ตัวอย่างเช่น การเคลื่อนที่ของวิถีกระสุนปืนใหญ่
หรือแม้แต่การเคลื่อนที่ของดาวเทียมรอบโลก ซึ่งโดยทั่วไปแล้ว
การหาการกระจัด ความเร็ว และความเร่ง ของการเคลื่อนที่
ในลักษณะดังกล่าว ก็สามารถประยุกต์ใช้สมการการเคลื่อนที่
ที่ได้นำเสนอในหัวข้อที่ผ่านมา สำหรับตัวอย่าง เฉพาะ
ของการเคลื่อนที่ในหลายมิติ ที่จะนำมาพิจารณาในบทนี้
ประกอบด้วยการเคลื่อนที่แบบโพรเจกไทล์ และ การเคลื่อนที่เป็นวงกลม
 1-4-1 การเคลื่อนที่แบบโพรเจกไทล์ (projectile
motion)
1-4-1 การเคลื่อนที่แบบโพรเจกไทล์ (projectile
motion) |
 |

การเคลื่อนที่แบบโพรเจกไทล์เป็นตัวอย่างหนึ่งของการเคลื่อนที่ใน
2 มิติ ที่มีแนวการเคลื่อนที่เป็นเส้นโค้ง กล่าวคือ
มีทั้งการเคลื่อนที่ในแนวระดับ และแนวดิ่งพร้อมๆกัน
โดยในแนวดิ่งวัตถุจะมีความเร่งคงตัว ซึ่งก็คือ ความเร่งเนื่องจากความโน้มถ่วงของโลกนั่นเอง
ในขณะที่ในแนวระดับ วัตถุมีความเร็วคงตัว สำหรับในตอนนี้
ในการคำนวณ จะไม่มีการนำผลของแรงต้านอากาศมาเกี่ยวข้อง

จากรูปที่
1-4 พิจารณาที่เวลา t = 0 อนุภาคเคลื่อนที่ออกจากจุดกำเนิด
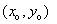
ด้วยความเร็วต้น u โดยมุมระหว่างเวกเตอร์ความเร็ว
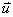
กับแกน x มีค่า
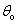

ดังนั้นที่จุดกำเนิด
ขนาดของความเร็วในแนวแกน เขียนได้เป็น
 เนื่องจากไม่มีความเร่งในแนวแกน x เพราะไม่คิดแรงต้านของอากาศ
ขนาดของความเร็วในแนวนอนที่เวลาต่างๆ จึงเป็นค่าคงที่
และสามารถเขียนได้เป็น
เนื่องจากไม่มีความเร่งในแนวแกน x เพราะไม่คิดแรงต้านของอากาศ
ขนาดของความเร็วในแนวนอนที่เวลาต่างๆ จึงเป็นค่าคงที่
และสามารถเขียนได้เป็น
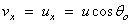
= ค่าคงที่ |
(1-27)
|
 ขนาดของความเร็วในแนวแกน y เขียนได้เป็น
ขนาดของความเร็วในแนวแกน y เขียนได้เป็น

ขนาดของความเร็วปลายในแนวแกน
y ณ เวลา t ใดๆ เขียนได้เป็น

จากสมการที่
(1-24) การกระจัดในแนวแกน x เขียนได้เป็น

และการกระจัดในแนวแกน
y เขียนได้เป็น

สังเกตว่าจากสมการที่
(1-27) ขนาดความเร็วในแนวแกน x มีค่าคงตัวไม่ขึ้นกับเวลา
เนื่องจากไม่มีความเร่ง ในแนวแกนนี้ แต่ความเร็วในแนวแกน
y จะมีการเปลี่ยนแปลงลดลงจนเป็นศูนย์ ณ จุดสูงสุด จากนั้นเมื่อวัตถุตกกลับลงมา
ก็จะมีความเร็วเพิ่มขึ้น (พิจารณาตามสมการที่ (1-29))

สำหรับความเร็วลัพธ์
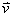
ณ เวลา t ใดๆ หาได้จาก

โดยขนาดของ
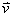
คือ

และทิศทางของเวกเตอร์
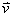
วัดเทียบกับแกน x หาได้จาก

จากรูปที่
1-5 แสดงกราฟการเคลื่อนที่ของวัตถุในแบบโพรเจกไทล์ สังเกตว่าวัตถุเริ่มเคลื่อนที่จาก
(0,0) เมื่อเวลา t = 0 ด้วยขนาดความเร็วต้น u เมื่อวัตถุเคลื่อนที่ไปถึงจุดยอดสุด
เมื่อเวลา
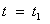
ความเร็วของวัตถุในแนวแกน
y ลดลงเป็นศูนย์ ระยะทางที่วัตถุเคลื่อนที่ได้ในแนวแกน
y คือ h และระยะทางที่วัตถุเคลื่อนที่ได้ในแนวแกน x
คือ
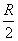

เมื่อวัตถุเคลื่อนที่ลง
ระยะทางของวัตถุในแนวแกน y จะลดลงจนเป็นศูนย์ ในขณะที่ระยะทางในแนวแกน
x มีค่าเป็น R เมื่อเวลาผ่านไป
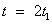

ในที่นี้
h บอกถึงความสูงที่วัตถุขึ้นไปได้สูงสุด (height) และ
R บอกถึงระยะทางที่วัตถุไปได้ไกลสุด (range) โดยค่า
h และ R สามารถเขียนให้อยู่ในรูปของ
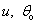
และ g ได้ดังนี้

เริ่มจากการพิจารณา
เมื่อวัตถุเคลื่อนที่ขึ้นไปถึงจุดสูงสุด จะได้ว่า
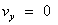
ดังนั้นเวลาที่วัตถุใช้ในการเคลื่อนที่จากจุดเริ่มต้น
ไปยังจุดสูงสุด ดังกล่าวหาได้โดยใช้สมการที่ (1-29)
หาได้จาก

แทนสมการที่
(1-35) ลงในสมการที่ (1-31) เพื่อหาความสูงที่วัตถุขึ้นไปได้สูงที่สุด
h

สำหรับระยะทางที่วัตถุไปได้ไกลที่สุด
สามารถหาได้จากสมการที่ (1-30) โดยแทนค่าเวลา ในสมการดังกล่าว
ด้วยค่าสองเท่าของเวลา ที่วัตถุใช้ในการเคลื่อนที่ขึ้นไปได้สูงสุด

ดังนั้น

สมการที่
(1-37) แสดงให้เห็นถึงค่าของ R ในรูปของ
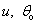
และ g

ในกรณีที่เรากำหนดให้
u เป็นค่าคงที่ และเปลี่ยนมุม
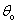
เท่านั้น จะพบว่า R จะมีค่ามากสุดเมื่อ สังเกตว่าที่มุม
45° วัตถุเคลื่อนที่ได้ระยะทางไกลที่สุด (ดูรูปที่
1-6)