(1-15)

(1-16)

        อนุภาคมีการเคลื่อนที่โดยตำแหน่ง ณ เวลาต่างๆ เป็นไปตามสมการ โดย มีหน่วยเป็นเมตร และ t มีหน่วยเป็นวินาที จงหา
        (ก) ความเร็วของอนุภาคที่ t=5 s
        (ข) ความเร่งเฉลี่ยของอนุภาคในช่วง t=5 s จนถึง t= 7 s
        (ค) ความเร่งของอนุภาคที่เวลา t=5 s

        วิธีทำ
        (ก) ความเร็วของอนุภาคที่ t=5 s

        (ข) ความเร่งเฉลี่ยของอนุภาคในช่วง t=5 s จนถึง t= 7 s

        (ค) ความเร่งของอนุภาคที่เวลา t=5 s

        หมายเหตุ ในตัวอย่างนี้ เวกเตอร์บอกตำแหน่งมีเฉพาะองค์ประกอบในแนวแกน x เท่านั้น จึงอาจจะละไม่เขียน แล้วใช้ แทน ได้

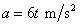
        อนุภาคมีการเคลื่อนที่ในหนึ่งมิติโดยมีความเร่ง ณ เวลาต่างๆ เป็นไปตามสมการ โดย t มีหน่วยเป็นวินาที และตอนเริ่มต้นที่เวลา t = 0 อนุภาคมีความเร็ว = 4 m/s และอยู่ที่ตำแหน่ง x = 0 m จงหา์

        (ก) ความเร็วของอนุภาคที่ t = 5 s
        (ข) ความเร่งเฉลี่ยของอนุภาคในช่วง t = 5 s จนถึง t = 7 s
        (ค) ตำแหน่งของอนุภาคที่เวลา t = 5 s
        (ง) ความเร็วเฉลี่ยของอนุภาคในช่วง t = 1 s จนถึง t = 3 s

        วิธีทำ

        (ก) ความเร็วของอนุภาคที่ t = 5 s
        โดยที่ c คือค่าคงที่ (arbitrary constant) ซึ่งเราจะหาค่า c ได้จากเงื่อนไข ที่โจทย์กำหนดให้ ว่า
(0) = 4m/s ทำให้ได้ว่า


        ดังนั้นจะได้ว่า

        ความเร็วของอนุภาคที่ t = 5 s คือ


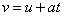
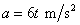
        หมายเหตุ นักศึกษาที่ลองทำข้อนี้ด้วยวิธีอื่น แล้วได้คำตอบเป็น 154 m/s นั้นเป็นคำตอบที่ผิด เพราะว่า นักศึกษาได้ใช้สูตรซึ่งไม่สามารถนำมาใช้ได้ สูตร   นั้น ใช้ได้เฉพาะกรณีที่ a เป็นค่าคงที่เท่านั้น (มัธยมปลาย) ส่วนในข้อนี้ (มหาวิทยาลัย) นั้น ซึ่งความเร่งเป็นฟังก์ชันของเวลาไม่ใช่ค่าคงที่ นักศึกษาจึงควรระวัง อย่าใช้สี่สูตร ระดับมัธยมปลายกับโจทย์ที่ความเร่งไม่คงที่อีก

          (ข) ความเร่งเฉลี่ยของอนุภาคในช่วง t = 5 s จนถึง t = 7 s


        (ค) ตำแหน่งของอนุภาคที่เวลา t = 5 s
        ในทำนองเดียวกับข้อ ก 


        โดยที่ c คือค่าคงที่ ซึ่งเราจะหาค่า c ได้จากเงื่อนไขที่โจทย์กำหนดให้ว่า x(0) = 0 m ทำให้ได้ว่า

        ดังนั้นจะได้ว่า

        ตำแหน่งของอนุภาคที่ t = 5 s คือ

        (ง) ความเร็วเฉลี่ยของอนุภาคในช่วง t = 1 s จนถึง t = 3 s