1-3-3 การเคลื่อนที่ด้วยความเร่งคงตัว

ในตอนนี้จะเป็นการหาสมการแสดงความสัมพันธ์ระหว่าง ความเร็ว ความเร่ง และ การกระจัด ในกรณีของความเร่งคงตัวในหนึ่งมิติ คล้ายเนื้อหาในระดับมัธยมปลาย โดยเริ่มพิจารณาจากขนาดของความเร็วเฉลี่ยตามสมการที่ (1-8)

ดังนั้น

(1-17)

หรือ

(1-18)

โดยที่
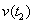
คือ ความเร็วปลาย ที่ระดับมัธยมปลายใช้
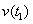
คือ ความเร็วต้น ที่ระดับมัธยมปลายใช้ u
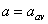
เป็นความเร่งซึ่งต้องเป็นค่าคงตัวเท่านั้น ความเร่งเฉลี่ย จึงเท่ากับความเร่งขณะใดขณะหนึ่ง
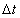
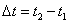
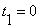
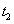
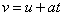
คือ ช่วงเวลาที่วัตถุเคลื่อนที่ ซึ่ง โดยในระดับมัธยมปลายนิยมเลือกให้ และเรียก ด้วย t จนเหลือสูตร แต่ในที่นี้จะยังคงไว้ในรูปของ

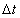
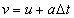
สำหรับกราฟสัมพันธ์ระหว่าง และ t ตามสมการ สามารถแสดงได้ดังรูปที่ 1-3

รูปที่ 1-3 แสดงความสัมพันธ์ระหว่าง และ t ตามสมการ

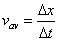
จากสมการ โดยที่ Δx คือกระจัดในช่วงเวลา Δt จะเห็นว่า ถ้าต้องการทราบความเร็วเฉลี่ย จะต้องทราบการกระจัดก่อน ซึ่งการกระจัด จะหาได้ง่ายในกรณีที่ความเร็วมีค่าคงตัว โดยการกระจัดก็คือผลคูณของความเร็วกับเวลา แต่หากว่าความเร็วไม่คงตัว เช่น กรณีที่มีความเร่งเหมือนในขณะนี้ เราจะต้องแยกคิดเวลาทีละส่วนย่อยๆ ซึ่งในแต่ละส่วนนั้น เล็กพอที่จะประมาณได้ว่า ความเร็วคงตัวแล้วจึงรวมการกระจัดทั้งหมด ซึ่งเราสามารถแสดงว่า การกระจัดทั้งหมดก็คือพื้นที่ใต้กราฟระหว่าง และ นั่นเอง

สำหรับในกรณีดังรูปที่ 1-3 จะได้ว่า
การกระจัด = พื้นที่ใต้กราฟ =พื้นที่สี่เหลี่ยมคางหมู =
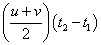
นั่นคือ

	(1-19)

เราสามารถใช้ผลจากสมการที่ (1-19) ร่วมกับนิยามของความเร็วเฉลี่ย ทำให้เราสามารถหาความเร็วเฉลี่ยได้เป็น


นั่นคือความเร็วเฉลี่ยมีค่าเป็น

(1-20)

ควรจะจำว่าความเร็วเฉลี่ยตามสมการที่ (1-20) นั้นเป็นจริง โดยมีเงื่อนไขว่าความเร่งต้องคงตัวเท่านั้น

แทนสมการที่ (1-18) ลงในสมการที่ (1-19) ทำให้สามารถเขียนการกระจัด Δx ได้เป็น

(1-21)

สมการที่ (1-21) แสดงถึงความสัมพันธ์ระหว่างการกระจัดกับเวลา
เนื่องจากสมการที่ (1-12) สามารถเขียนได้เป็น

(1-22)

แทนสมการที่ (1-22) ลงในสมการที่ (1-19) จะได้สมการของการกระจัด ในอีกรูปแบบหนึ่งดังนี้


หรือ

(1-23)

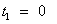
หมายเหตุ ในระดับมัธยมปลายนิยมกำหนดให้เวลาเริ่มต้น แทน ด้วย t และแทน Δx ด้วยการกระจัด s ทำให้สมการที่ (1-21) เขียนใหม่ได้เป็น

(1-24)

และ สมการที่ (1-23) เขียนใหม่ได้เป็น

(1-25)