 หลายๆคนคงมีประสบการณ์มาบ้างแล้วว่า
ในการที่จะหยุดวัตถุ ที่กำลังเคลื่อนที่ ความเร็วไม่ใช่เพียงปัจจัยเดียว
ที่มีผลต่อการออกแรงต้านการเคลื่อนที่เพื่อให้วัตถุหยุด
โดยในความเป็นจริงแล้ว มวลของวัตถุ ก็มีผลต่อการออกแรงต้าน
ด้วยเช่นกัน ตัวอย่างเช่น ความพยายามในการออกแรงต้านการเคลื่อนที่
เพื่อทำการหยุดรถจักรยานเทียบกับรถยนต์ ในช่วงเวลาเท่าๆกัน
โดยทั้งคู่มีความเร็วเท่ากัน จะพบว่า แรงต้านที่ใช้
มีความแตกต่างกันเป็นอย่างมาก เนื่องจากของทั้งสองสิ่งมีมวลต่างกันอย่างมาก
ปริมาณที่แสดงถึงความสัมพันธ์ ระหว่างความเร็วและมวลของวัตถ
ุที่กำลังเคลื่อนที่ เรียกว่า โมเมนตัม ซึ่งบางครั้งก็จะเรียกปริมาณนั้นให้เฉพาะลงไปว่า
โมเมนตัมเชิงเส้น หลายๆคนคงมีประสบการณ์มาบ้างแล้วว่า
ในการที่จะหยุดวัตถุ ที่กำลังเคลื่อนที่ ความเร็วไม่ใช่เพียงปัจจัยเดียว
ที่มีผลต่อการออกแรงต้านการเคลื่อนที่เพื่อให้วัตถุหยุด
โดยในความเป็นจริงแล้ว มวลของวัตถุ ก็มีผลต่อการออกแรงต้าน
ด้วยเช่นกัน ตัวอย่างเช่น ความพยายามในการออกแรงต้านการเคลื่อนที่
เพื่อทำการหยุดรถจักรยานเทียบกับรถยนต์ ในช่วงเวลาเท่าๆกัน
โดยทั้งคู่มีความเร็วเท่ากัน จะพบว่า แรงต้านที่ใช้
มีความแตกต่างกันเป็นอย่างมาก เนื่องจากของทั้งสองสิ่งมีมวลต่างกันอย่างมาก
ปริมาณที่แสดงถึงความสัมพันธ์ ระหว่างความเร็วและมวลของวัตถ
ุที่กำลังเคลื่อนที่ เรียกว่า โมเมนตัม ซึ่งบางครั้งก็จะเรียกปริมาณนั้นให้เฉพาะลงไปว่า
โมเมนตัมเชิงเส้น
 นิยามสำหรับโมเมนตัมเชิงเส้นของวัตถุมวล
m เคลื่อนที่ด้วยความเร็ว นิยามสำหรับโมเมนตัมเชิงเส้นของวัตถุมวล
m เคลื่อนที่ด้วยความเร็ว 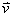 เขียนได้ดังนี้
เขียนได้ดังนี้
 โมเมนตัมนี้เป็นปริมาณเวกเตอร์
มีหน่วยในระบบ SI เป็น kg ms-1 โมเมนตัมนี้เป็นปริมาณเวกเตอร์
มีหน่วยในระบบ SI เป็น kg ms-1
 ดังนั้นจากตัวอย่างที่ยกมาแสดงว่า
รถจักรยานและรถยนต์ที่มีความเร็วเท่ากันแต่มีโมเมนตัมที่ต่างกัน
เนื่องจากรถยนต์มีมวลมากกว่า จึงมีโมเมนตัมมากกว่ารถจักรยาน ดังนั้นจากตัวอย่างที่ยกมาแสดงว่า
รถจักรยานและรถยนต์ที่มีความเร็วเท่ากันแต่มีโมเมนตัมที่ต่างกัน
เนื่องจากรถยนต์มีมวลมากกว่า จึงมีโมเมนตัมมากกว่ารถจักรยาน
 ถ้าการเคลี่อนที่ของวัตถุมวล
m เทียบกับจุดกำเนิดในพิกัดฉาก xyz โมเมนตัม ถ้าการเคลี่อนที่ของวัตถุมวล
m เทียบกับจุดกำเนิดในพิกัดฉาก xyz โมเมนตัม 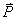 สามารถเขียนได้เป็น
ผลรวมของโมเมนตัมเชิงเส้น จากส่วนประกอบย่อยทั้งสามในพิกัดฉากได้ดังนี้ สามารถเขียนได้เป็น
ผลรวมของโมเมนตัมเชิงเส้น จากส่วนประกอบย่อยทั้งสามในพิกัดฉากได้ดังนี้
 กฎการเคลื่อนที่ข้อที่สองของนิวตัน
ได้ให้ความสัมพันธ์ระหว่างแรง กฎการเคลื่อนที่ข้อที่สองของนิวตัน
ได้ให้ความสัมพันธ์ระหว่างแรง 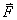 และโมเมนตัม และโมเมนตัม
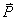 ตามสมการที่ 2-3 ดังนี้
ตามสมการที่ 2-3 ดังนี้
 สมการที่
(4-3) แสดงถึงอัตราการเปลี่ยนแปลงโมเมนตัมของวัตถุมวล
m มีค่าเท่ากับแรงภายนอกที่กระทำลงบนวัตถุนั้น นอกจากนี้จะสังเกตได้ว่าถ้าไม่มีแรงภายนอกมากระทำต่อวัตถุ สมการที่
(4-3) แสดงถึงอัตราการเปลี่ยนแปลงโมเมนตัมของวัตถุมวล
m มีค่าเท่ากับแรงภายนอกที่กระทำลงบนวัตถุนั้น นอกจากนี้จะสังเกตได้ว่าถ้าไม่มีแรงภายนอกมากระทำต่อวัตถุ
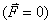 โมเมนตัม
โมเมนตัม 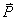 จะคงตัว
หมายความว่าไม่มีการเปลี่ยนแปลงโมเมนตัมเมื่อเทียบกับเวลา
หรือกล่าวอีกนัยหนึ่งคือเมื่อ จะคงตัว
หมายความว่าไม่มีการเปลี่ยนแปลงโมเมนตัมเมื่อเทียบกับเวลา
หรือกล่าวอีกนัยหนึ่งคือเมื่อ 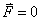 วัตถุจะเคลื่อนที่ด้วยความเร็วคงตัว
วัตถุจะเคลื่อนที่ด้วยความเร็วคงตัว
 สมการที่
(4-3) สามารถเขียนได้เป็น สมการที่
(4-3) สามารถเขียนได้เป็น
 เมื่อทำการ
integrate สมการที่ 4-4 โดยกำหนด limit ของการ integrate
ดังนี้ เมื่อทำการ
integrate สมการที่ 4-4 โดยกำหนด limit ของการ integrate
ดังนี้
 ณ
เวลา ณ
เวลา 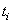 โมเมนตัมของวัตถุมีค่า
โมเมนตัมของวัตถุมีค่า 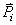 และเมื่อเวลาผ่านไปเป็น
และเมื่อเวลาผ่านไปเป็น 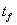 โมเมนตัมของวัตถุเปลี่ยนไปเป็น โมเมนตัมของวัตถุเปลี่ยนไปเป็น
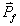 ดังนั้น
ดังนั้น
 ปริมาณที่อยู่ทางขวามือของสมการที่
(4-5) เรียกว่า การดล (impulse) ของแรง ปริมาณที่อยู่ทางขวามือของสมการที่
(4-5) เรียกว่า การดล (impulse) ของแรง 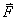 สำหรับช่วงเวลา สำหรับช่วงเวลา
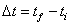 โดยมีการกำหนดสัญลักษณ์ของ impulse ให้เป็น J ดังนั้น
โดยมีการกำหนดสัญลักษณ์ของ impulse ให้เป็น J ดังนั้น
 กล่าวโดยสรุปคือ
การดลเนื่องจากแรงดล กล่าวโดยสรุปคือ
การดลเนื่องจากแรงดล 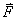 ที่กระทำต่อวัตถุ
มีค่าเท่ากับการเปลี่ยนแปลงโมเมนตัมของวัตถุ ซึ่งข้อสรุปดังกล่าวเรียกว่าเป็น
impulse - momentum theorem ที่กระทำต่อวัตถุ
มีค่าเท่ากับการเปลี่ยนแปลงโมเมนตัมของวัตถุ ซึ่งข้อสรุปดังกล่าวเรียกว่าเป็น
impulse - momentum theorem
 การดลเป็นปริมาณเวกเตอร์
เช่นเดียวกับโมเมนตัม ซึ่งถ้าสังเกตจากสมการที่ (4-6)
จะพบว่าขนาดการดลก็คือพื้นที่ใต้กราฟของแรงกับเวลานั่นเอง
ซึ่งหากเราทราบว่า การดลเป็นปริมาณเวกเตอร์
เช่นเดียวกับโมเมนตัม ซึ่งถ้าสังเกตจากสมการที่ (4-6)
จะพบว่าขนาดการดลก็คือพื้นที่ใต้กราฟของแรงกับเวลานั่นเอง
ซึ่งหากเราทราบว่า 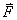 ขึ้นกับเวลาอย่างไรก็สามารถที่จะอินทิเกรตหาค่าของพื้นที่ใต้กราฟได้ ขึ้นกับเวลาอย่างไรก็สามารถที่จะอินทิเกรตหาค่าของพื้นที่ใต้กราฟได้
|