 นิยามศัพท์
นิยามศัพท์ |
|
 ก่อนที่จะศึกษาต่อไป
เราต้องทำความเข้าใจกับศัพท์ต่อไปนี้ที่เราจะพบบ่อย ๆ ในเรื่องของเทอร์โมไดนามิกส์ ก่อนที่จะศึกษาต่อไป
เราต้องทำความเข้าใจกับศัพท์ต่อไปนี้ที่เราจะพบบ่อย ๆ ในเรื่องของเทอร์โมไดนามิกส์
 เทอร์โมไดนามิกส์เป็นการศึกษาเกี่ยวกับการเปลี่ยนแปลงสภาวะ
(state) ของระบบ
(system) โดยที่ระบบคือส่วนหรือบริเวณของ
space หรือสสาร (matter) ที่เรากำลังศึกษา ที่ถูกแยกออกจากสิ่งที่อยู่รอบ
ๆ ซึ่งมีผลต่อพฤติกรรมของระบบ สิ่งที่อยู่รอบ ๆ นี้เรียกว่า
สิ่งแวดล้อม (surrounding)
ผิวซึ่งแยกระบบกับสิ่งแวดล้อมออกจากกันเรียกว่า
ขอบเขต (boundary)
ของระบบ ซึ่งเราอาจมองเห็นได้หรืออาจเป็นแค่ขอบเขตที่เราสมมุติขึ้นมาในมโนภาพ
(imaginary) เทอร์โมไดนามิกส์เป็นการศึกษาเกี่ยวกับการเปลี่ยนแปลงสภาวะ
(state) ของระบบ
(system) โดยที่ระบบคือส่วนหรือบริเวณของ
space หรือสสาร (matter) ที่เรากำลังศึกษา ที่ถูกแยกออกจากสิ่งที่อยู่รอบ
ๆ ซึ่งมีผลต่อพฤติกรรมของระบบ สิ่งที่อยู่รอบ ๆ นี้เรียกว่า
สิ่งแวดล้อม (surrounding)
ผิวซึ่งแยกระบบกับสิ่งแวดล้อมออกจากกันเรียกว่า
ขอบเขต (boundary)
ของระบบ ซึ่งเราอาจมองเห็นได้หรืออาจเป็นแค่ขอบเขตที่เราสมมุติขึ้นมาในมโนภาพ
(imaginary)
 พฤติกรรมหรือการเปลี่ยนแปลงสภาวะของระบบอาจบรรยายได้โดยใช้ปริมาณเชิงมหภาพ
(macroscopic quantities) เช่นความดัน ปริมาตร อุณหภูมิและมวลของระบบ
นอกจากนี้ยังสามารถบรรยายได้โดยใช้ปริมาณเชิงจุลภาพ
(microscopic quantities)
เช่น มวล อัตราเร็ว พลังงานจลน์และโมเมตัมของแต่ละโมเลกุลที่ประกอบกันขึ้นมาเป็นสสารหรือระบบที่เรากำลังศึกษา
ปริมาณทั้งสองนี้เกี่ยวข้องซึ่งกันและกัน เช่นแรงที่เกิดขึ้นเมื่อโมเลกุลของอากาศวิ่งชนกับผิวของของแข็ง
(แรงนี้เป็นปริมาณเชิงจุลภาพ) ทำให้เกิดความดันบรรยากาศ (ซึ่งเป็นปริมาณเชิงมหภาพ) พฤติกรรมหรือการเปลี่ยนแปลงสภาวะของระบบอาจบรรยายได้โดยใช้ปริมาณเชิงมหภาพ
(macroscopic quantities) เช่นความดัน ปริมาตร อุณหภูมิและมวลของระบบ
นอกจากนี้ยังสามารถบรรยายได้โดยใช้ปริมาณเชิงจุลภาพ
(microscopic quantities)
เช่น มวล อัตราเร็ว พลังงานจลน์และโมเมตัมของแต่ละโมเลกุลที่ประกอบกันขึ้นมาเป็นสสารหรือระบบที่เรากำลังศึกษา
ปริมาณทั้งสองนี้เกี่ยวข้องซึ่งกันและกัน เช่นแรงที่เกิดขึ้นเมื่อโมเลกุลของอากาศวิ่งชนกับผิวของของแข็ง
(แรงนี้เป็นปริมาณเชิงจุลภาพ) ทำให้เกิดความดันบรรยากาศ (ซึ่งเป็นปริมาณเชิงมหภาพ)
 เราจะใช้ปริมาณเหล่านี้ในการศึกษาสมบัติทางความร้อนของสสาร
สสารหนึ่งที่ง่ายที่สุดในการศึกษาคือ แก๊สอุดมคติ
(ideal gas) ซึ่งเป็นแก๊สที่ไม่มีอยู่จริง ประกอบด้วยโมเลกุลขนาดเล็กมาก
(เรียกว่า point-like particle) ที่เหมือนกันเป็นจำนวนมาก จนสามารถถือได้ว่าการกระจายความเร็วของโมเลกุลมีค่าคงที่
ระหว่างการเคลื่อนที่ของโมเลกุลของแก๊สอุดมคติจะมีแรงเกิดขึ้นเฉพาะเมื่อเกิดการชนระหว่างโมเลกุลด้วยกัน
หรือเมื่อโมเลกุลชนกับผนังภาชนะเท่านั้น จะไม่มีแรงระหว่างโมเลกุล เราจะใช้ปริมาณเหล่านี้ในการศึกษาสมบัติทางความร้อนของสสาร
สสารหนึ่งที่ง่ายที่สุดในการศึกษาคือ แก๊สอุดมคติ
(ideal gas) ซึ่งเป็นแก๊สที่ไม่มีอยู่จริง ประกอบด้วยโมเลกุลขนาดเล็กมาก
(เรียกว่า point-like particle) ที่เหมือนกันเป็นจำนวนมาก จนสามารถถือได้ว่าการกระจายความเร็วของโมเลกุลมีค่าคงที่
ระหว่างการเคลื่อนที่ของโมเลกุลของแก๊สอุดมคติจะมีแรงเกิดขึ้นเฉพาะเมื่อเกิดการชนระหว่างโมเลกุลด้วยกัน
หรือเมื่อโมเลกุลชนกับผนังภาชนะเท่านั้น จะไม่มีแรงระหว่างโมเลกุล
UP
 |
 สมการของสภาวะ
(equation of state) สมการของสภาวะ
(equation of state) |
|
 สิ่งที่ใช้ในการบอกสภาวะของระบบหรือสสารหนึ่ง
ๆ คือ ตัวแปรสภาวะ (state variables)
อันได้แก่ ความดัน p ปริมาตร V อุณหภูมิ T
และมวล m (หรืออาจใช้จำนวนโมล n) โดยทั่วไป ถ้าตัวแปรหนึ่งมีค่าเปลี่ยนไป
ตัวแปรอื่น ๆ อย่างน้อยหนึ่งตัวแปรจะมีค่าเปลี่ยนไปด้วย ถ้าความสัมพันธ์ของตัวแปรเหล่านี้เป็นไปอย่างง่าย
ๆ เราสามารถเขียนความสัมพันธ ์ออกมาในรูปของสมการที่เรียกว่า สมการของสภาวะ
(equation of state) ได้ แต่ถ้ายากเกินไป เราอาจบรรยายด้วยกราฟหรือตาราง สิ่งที่ใช้ในการบอกสภาวะของระบบหรือสสารหนึ่ง
ๆ คือ ตัวแปรสภาวะ (state variables)
อันได้แก่ ความดัน p ปริมาตร V อุณหภูมิ T
และมวล m (หรืออาจใช้จำนวนโมล n) โดยทั่วไป ถ้าตัวแปรหนึ่งมีค่าเปลี่ยนไป
ตัวแปรอื่น ๆ อย่างน้อยหนึ่งตัวแปรจะมีค่าเปลี่ยนไปด้วย ถ้าความสัมพันธ์ของตัวแปรเหล่านี้เป็นไปอย่างง่าย
ๆ เราสามารถเขียนความสัมพันธ ์ออกมาในรูปของสมการที่เรียกว่า สมการของสภาวะ
(equation of state) ได้ แต่ถ้ายากเกินไป เราอาจบรรยายด้วยกราฟหรือตาราง
  สมการของสภาวะสำหรับแก๊สอุดมคติ (the ideal gas equation)
สมการของสภาวะสำหรับแก๊สอุดมคติ (the ideal gas equation)
 สมการของสภาวะที่ง่ายที่สุดอันหนึ่งคือ
สมการของสภาวะสำหรับแก๊สอุดมคติ เราจะใช้จำนวนโมล สมการของสภาวะที่ง่ายที่สุดอันหนึ่งคือ
สมการของสภาวะสำหรับแก๊สอุดมคติ เราจะใช้จำนวนโมล 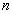 ในการบอกปริมาณของแก๊สแทนที่จะใช้มวล m โดยที่
ในการบอกปริมาณของแก๊สแทนที่จะใช้มวล m โดยที่
 เมื่อ เมื่อ
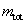 คือมวลทั้งหมดของสสารในระบบที่เราสนใจ
คือมวลทั้งหมดของสสารในระบบที่เราสนใจ
 M
คือมวลโมลาร์หรือมวลต่อโมลของสสาร M
คือมวลโมลาร์หรือมวลต่อโมลของสสาร
จากการทดลองหาความสัมพันธ์ของตัวแปรสภาวะต่าง ๆ จะพบว่า

 ปริมาตร ปริมาตร
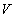 แปรผันตรงกับจำนวนโมล n เช่นถ้าเราเพิ่มจำนวนโมลเป็นสองเท่า โดยควบคุมให้ความดันและอุณหภูมิคงที่
ปริมาตรจะเพิ่มเป็นสองเท่าด้วย
แปรผันตรงกับจำนวนโมล n เช่นถ้าเราเพิ่มจำนวนโมลเป็นสองเท่า โดยควบคุมให้ความดันและอุณหภูมิคงที่
ปริมาตรจะเพิ่มเป็นสองเท่าด้วย

 ปริมาตร ปริมาตร
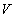 แปรผกผันกับความดันสัมบูรณ์ (absolute pressure) p เช่นถ้าเราเพิ่มความดันเป็นสองเท่าโดยควบคุมอุณหภูมิและจำนวนโมลให้คงที่
แก๊สจะถูกกดให้มีปริมาตรลดลงครึ่งหนึ่ง นั่นคือ
แปรผกผันกับความดันสัมบูรณ์ (absolute pressure) p เช่นถ้าเราเพิ่มความดันเป็นสองเท่าโดยควบคุมอุณหภูมิและจำนวนโมลให้คงที่
แก๊สจะถูกกดให้มีปริมาตรลดลงครึ่งหนึ่ง นั่นคือ 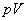 = ค่าคงที่ เมื่อ
= ค่าคงที่ เมื่อ 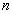 และ
และ 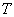 คงที่
คงที่
  ความดัน
ความดัน 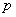 แปรผันตรงกับอุณหภูมิสัมบูรณ์หรืออุณหภูมิในสเกลเคลวิน
แปรผันตรงกับอุณหภูมิสัมบูรณ์หรืออุณหภูมิในสเกลเคลวิน 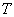 เช่นถ้าเราเพิ่มอุณหภูมิสัมบูรณ์ขึ้นเป็นสองเท่า โดยควบคุมให้ปริมาตรและจำนวนโมลมีค่าคงที่
ความดันจะเพิ่มขึ้นเป็นสองเท่าเช่นกัน นั่นคือ
เช่นถ้าเราเพิ่มอุณหภูมิสัมบูรณ์ขึ้นเป็นสองเท่า โดยควบคุมให้ปริมาตรและจำนวนโมลมีค่าคงที่
ความดันจะเพิ่มขึ้นเป็นสองเท่าเช่นกัน นั่นคือ 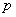 = (ค่าคงที่)
= (ค่าคงที่) 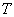 เมื่อ
เมื่อ 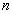 และ
และ 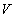 คงที่
คงที่
 จากความสัมพันธ์เหล่านี้
เราสามารถเขียนรวมให้อยู่ในสมการเดียวกันได้ เรียกว่า
ideal-gas equation: จากความสัมพันธ์เหล่านี้
เราสามารถเขียนรวมให้อยู่ในสมการเดียวกันได้ เรียกว่า
ideal-gas equation:
 เมื่อ เมื่อ
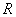 คือค่าคงที่
ซึ่งมีค่าเท่ากันหมดสำหรับแก๊สทุกชนิด (ที่อุณหภูมิสูงและความดันต่ำพอเหมาะ)
มันจึงถูกเรียกว่า ค่าคงที่สากลของแก๊ส
(universal gas constant) โดยที่ คือค่าคงที่
ซึ่งมีค่าเท่ากันหมดสำหรับแก๊สทุกชนิด (ที่อุณหภูมิสูงและความดันต่ำพอเหมาะ)
มันจึงถูกเรียกว่า ค่าคงที่สากลของแก๊ส
(universal gas constant) โดยที่
 (ค่า (ค่า
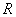 นี้ใช้กับความดันและปริมาตรที่มีหน่วยในระบบ SI เป็น N/m2
และ m3 ตามลำดับ)
นี้ใช้กับความดันและปริมาตรที่มีหน่วยในระบบ SI เป็น N/m2
และ m3 ตามลำดับ)
 เราสามารถเขียน
ideal-gas equation ในรูปของมวลทั้งหมด เราสามารถเขียน
ideal-gas equation ในรูปของมวลทั้งหมด 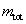 ของระบบได้โดยใช้สมการ (9-26) นั่นคือ
ของระบบได้โดยใช้สมการ (9-26) นั่นคือ
 สำหรับระบบที่มีมวลของแก๊สอุดมคติ
(หรือจำนวนโมลคงที่) ผลคูณ สำหรับระบบที่มีมวลของแก๊สอุดมคติ
(หรือจำนวนโมลคงที่) ผลคูณ 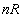 จะคงที่ และ
จะคงที่ และ 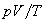 จึงคงที่ด้วย ดังนั้นระบบที่มีมวลของแก๊สอุดมคติคงที่ในสองสภาวะที่ต่างกัน
(สภาวะที่ 1 และสภาวะที่ 2) จะได้
จึงคงที่ด้วย ดังนั้นระบบที่มีมวลของแก๊สอุดมคติคงที่ในสองสภาวะที่ต่างกัน
(สภาวะที่ 1 และสภาวะที่ 2) จะได้
  อุณหภูมิและความดันมาตรฐาน (Standard Temperature and Pressure: STP)
อุณหภูมิและความดันมาตรฐาน (Standard Temperature and Pressure: STP)
 สำหรับแก๊สที่
STP หมายถึงแก๊สที่อุณหภูมิ สำหรับแก๊สที่
STP หมายถึงแก๊สที่อุณหภูมิ 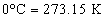 และที่ความดัน
และที่ความดัน 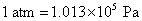 ดังนั้นปริมาตรที่ต้องใช้ในการบรรจุ ideal gas จำนวน 1 โมล ที่ STP
คือ
ดังนั้นปริมาตรที่ต้องใช้ในการบรรจุ ideal gas จำนวน 1 โมล ที่ STP
คือ
 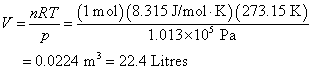
 นอกจากสมการของสภาวะสำหรับแก๊สอุดมคติสามารถเขียนอยู่ในเทอมของจำนวนโมลแล้ว
เราสามารถเขียนให้อยู่ในรูปของจำนวนโมเลกุลของแก๊สทั้งหมด นอกจากสมการของสภาวะสำหรับแก๊สอุดมคติสามารถเขียนอยู่ในเทอมของจำนวนโมลแล้ว
เราสามารถเขียนให้อยู่ในรูปของจำนวนโมเลกุลของแก๊สทั้งหมด 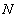 ได้ โดยพิจารณาดังนี้
ได้ โดยพิจารณาดังนี้
 จำนวนโมเลกุลทั้งหมด จำนวนโมเลกุลทั้งหมด
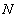 ในระบบที่เราศึกษาคือ จำนวนโมล n คูณด้วย เลขอโวกาโดร (Avogadros
number)
ในระบบที่เราศึกษาคือ จำนวนโมล n คูณด้วย เลขอโวกาโดร (Avogadros
number) 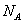 นั่นคือ
นั่นคือ
(9-29)
 เพราะ เพราะ
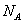 หมายถึงจำนวนโมเลกุลของแก๊สในหนึ่งโมล โดยที่
หมายถึงจำนวนโมเลกุลของแก๊สในหนึ่งโมล โดยที่
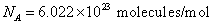
 (วิธีคิด:
แก๊ส 1 โมล มีโมเลกุลของแก๊สจำนวน (วิธีคิด:
แก๊ส 1 โมล มีโมเลกุลของแก๊สจำนวน 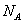 โมเลกุล ฉะนั้นแก๊ส
โมเลกุล ฉะนั้นแก๊ส 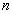 โมล จะมีโมเลกุลของแก๊สทั้งหมด
โมล จะมีโมเลกุลของแก๊สทั้งหมด 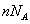 โมเลกุล)
โมเลกุล)
 ดังนั้น
จาก ดังนั้น
จาก 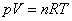 จะได้
จะได้
 เราเรียก เราเรียก
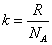 ว่า ค่าคงที่ของ Boltzmann โดยที่
ว่า ค่าคงที่ของ Boltzmann โดยที่
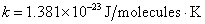 หรืออาจใช้สัญลักษณ์
หรืออาจใช้สัญลักษณ์ 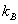 ) )
| |
 ตัวอย่างที่ 9-7
ตัวอย่างที่ 9-7 |
| |
ก) แก๊สอาร์กอน
1.00 m 3 ที่ STP มีกี่โมเลกุล
ข) แก๊สเรดอน
1.00 m 3ที่ STP มีกี่โมเลกุล
วิธีทำ
แก๊สทั้งสองชนิดมีปริมาตรเท่ากันจะมีจำนวนโมเลกุลเท่ากัน
ใช้สมการของสภาวะสำหรับแก๊สอุดมคติ
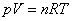
จะได้ว่า 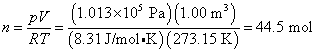
|
ดังนั้นจำนวนโมเลกุลทั้งหมดคือ
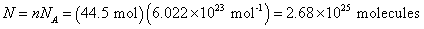
|
  สมการของ Van der Waals สำหรับแก๊สจริง
(Van der Waals equation for real gas)
สมการของ Van der Waals สำหรับแก๊สจริง
(Van der Waals equation for real gas)
 แก๊สจริง
(real gas) จะไม่ประพฤติตัวตามสมการของสภาวะสำหรับแก๊สอุดมคติได้ตามสมการ
(9-26) แต่หากแก๊สใดที่มีความดันน้อย ๆ เช่นน้อยกว่า 1 atm และมีอุณหภูมิสูงกว่าจุดเดือดของมันมาก
ๆ เราอาจสามารถใช้สมการของสภาวะสำหรับแก๊สอุดมคติข้างต้นในการบรรยายพฤติกรรมของแก๊สนั้นได้
นักฟิสิกส์ขาวเนเธอร์แลนด์ Johannes Van der Waals ได้เสนอไว้ในศตวรรษที่
19 ว่า สมการของสภาวะของแก๊สจริงจะอยู่ในรูป แก๊สจริง
(real gas) จะไม่ประพฤติตัวตามสมการของสภาวะสำหรับแก๊สอุดมคติได้ตามสมการ
(9-26) แต่หากแก๊สใดที่มีความดันน้อย ๆ เช่นน้อยกว่า 1 atm และมีอุณหภูมิสูงกว่าจุดเดือดของมันมาก
ๆ เราอาจสามารถใช้สมการของสภาวะสำหรับแก๊สอุดมคติข้างต้นในการบรรยายพฤติกรรมของแก๊สนั้นได้
นักฟิสิกส์ขาวเนเธอร์แลนด์ Johannes Van der Waals ได้เสนอไว้ในศตวรรษที่
19 ว่า สมการของสภาวะของแก๊สจริงจะอยู่ในรูป
 เมื่อ
a และ b คือค่าคงที่ที่ได้จากการทดลองซึ่งมีค่าต่างกันสำหรับแก๊สต่างชนิดกัน
โดยประมาณค่า b แทนปริมาตรของแก๊ส 1 โมล ดังนั้นปริมาตรรวมทั้งหมดของแก๊ส
n โมล คือ nb และทำให้ปริมาตรที่โมเลกุลสามารถเคลื่อนที่ไปได้ (free
volume) คือ เมื่อ
a และ b คือค่าคงที่ที่ได้จากการทดลองซึ่งมีค่าต่างกันสำหรับแก๊สต่างชนิดกัน
โดยประมาณค่า b แทนปริมาตรของแก๊ส 1 โมล ดังนั้นปริมาตรรวมทั้งหมดของแก๊ส
n โมล คือ nb และทำให้ปริมาตรที่โมเลกุลสามารถเคลื่อนที่ไปได้ (free
volume) คือ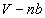 ส่วนค่าคงที่ a เกี่ยวข้องกับแรงดึงดูดระหว่างโมเลกุลที่อยู่ติดกัน
โดยขณะที่โมเลกุลชั้นหนึ่ง กำลังชนกับผนังภาชนะโมเลกุลในอีกชั้นหนึ่งที่อยู่ถัดไปจะไปดึงมันเข้าสู่ภายใน
ทำให้ความดันลดลง พบว่าความดันที่ลดลงแปรผันตรงกับ
ส่วนค่าคงที่ a เกี่ยวข้องกับแรงดึงดูดระหว่างโมเลกุลที่อยู่ติดกัน
โดยขณะที่โมเลกุลชั้นหนึ่ง กำลังชนกับผนังภาชนะโมเลกุลในอีกชั้นหนึ่งที่อยู่ถัดไปจะไปดึงมันเข้าสู่ภายใน
ทำให้ความดันลดลง พบว่าความดันที่ลดลงแปรผันตรงกับ 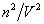
UP
 |
 กราฟระหว่างความดันกับปริมาตร
(pV -diagrams) กราฟระหว่างความดันกับปริมาตร
(pV -diagrams) |
|
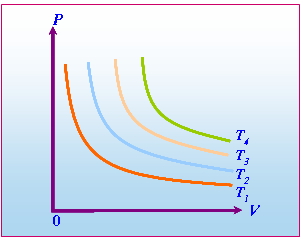
รูปที่ 9-4 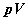 -Diagram
|
 เราสามารถบรรยายความสัมพันธ์ของ เราสามารถบรรยายความสัมพันธ์ของ
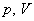 และ
และ 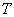 โดยใช้กราฟหรือแผนภาพเพื่อให้มองเห็นภาพของพฤติกรรมของระบบได้ง่ายขึ้น
เพื่อความสะดวกเรามักใช้แผนภาพใน 2 มิติ ตัวแปรที่นิยมใช้ในการเขียนกราฟหรือแผนภาพมากที่สุดคือ
ความดัน
โดยใช้กราฟหรือแผนภาพเพื่อให้มองเห็นภาพของพฤติกรรมของระบบได้ง่ายขึ้น
เพื่อความสะดวกเรามักใช้แผนภาพใน 2 มิติ ตัวแปรที่นิยมใช้ในการเขียนกราฟหรือแผนภาพมากที่สุดคือ
ความดัน 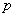 และ ปริมาตร
และ ปริมาตร 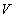 โดย
โดย 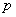 จะเป็นฟังก์ชันของ
จะเป็นฟังก์ชันของ 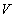 เรียกกราฟนี้ว่า
เรียกกราฟนี้ว่า 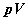 -diagram
แต่ละเส้นโค้งในแผนภาพจะแทนพฤติกรรมที่เกิดขึ้น ณ อุณหภูมิหนึ่ง ๆ เรียกเส้นโค้งนี้ว่า
isotherm หรือ -diagram
แต่ละเส้นโค้งในแผนภาพจะแทนพฤติกรรมที่เกิดขึ้น ณ อุณหภูมิหนึ่ง ๆ เรียกเส้นโค้งนี้ว่า
isotherm หรือ 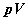 -isotherm
ตัวอย่างในรูปที่ 9-4 ซึ่งเป็น -isotherm
ตัวอย่างในรูปที่ 9-4 ซึ่งเป็น 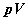 -diagram
สำหรับแก๊สอุดมคติจำนวนหนึ่งโดยที่ -diagram
สำหรับแก๊สอุดมคติจำนวนหนึ่งโดยที่ 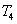 เป็นอุณหภูมิที่สูงที่สุด และ
เป็นอุณหภูมิที่สูงที่สุด และ 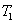 เป็นอุณหภูมิที่ต่ำที่สุด
เป็นอุณหภูมิที่ต่ำที่สุด
UP
 |
|














