 ในส่วนนี้จะเป็นการเขียนกฏของนิวตันสำหรับระบบอนุภาค
ซึ่งจะขอเริ่มต้น ด้วยการพิจารณาระบบสองอนุภาค แล้วจึงขยายไประบบที่มีหลายอนุภาค
ในส่วนนี้จะเป็นการเขียนกฏของนิวตันสำหรับระบบอนุภาค
ซึ่งจะขอเริ่มต้น ด้วยการพิจารณาระบบสองอนุภาค แล้วจึงขยายไประบบที่มีหลายอนุภาค
 จากสมการแสดงจุดศูนย์กลางมวลในรูปของเวกเตอร์
สมการที่ (5-1) จากสมการแสดงจุดศูนย์กลางมวลในรูปของเวกเตอร์
สมการที่ (5-1)
 ถ้าหาอนุพันธ์เทียบกับเวลาของสมการดังกล่าว
จะได้เป็น ถ้าหาอนุพันธ์เทียบกับเวลาของสมการดังกล่าว
จะได้เป็น
 หรือ หรือ
 ถ้าหาอนุพันธ์เทียบกับเวลาอีกครั้งหนึ่งจะได้เป็น ถ้าหาอนุพันธ์เทียบกับเวลาอีกครั้งหนึ่งจะได้เป็น
 เราสามารถทำกระบวนการเดียวกันนี้กับ เราสามารถทำกระบวนการเดียวกันนี้กับ
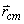 แทนที่จะเป็นแค่ แทนที่จะเป็นแค่
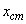 โดยเริ่มจากสมการแสดงจุดศูนย์กลางมวลในรูปของเวกเตอร์
สมการที่ (5-6) โดยเริ่มจากสมการแสดงจุดศูนย์กลางมวลในรูปของเวกเตอร์
สมการที่ (5-6)
 ถ้าหาอนุพันธ์เทียบกับเวลาของสมการดังกล่าว
จะได้เป็น ถ้าหาอนุพันธ์เทียบกับเวลาของสมการดังกล่าว
จะได้เป็น
 หรือ หรือ
 ทางด้านขวาของสมการที่ (5-15) คือผลรวมของโมเมนตัมสำหรับระบบซึ่งประกอบด้วย
n อนุภาค ซึ่งมีค่าเท่ากับโมเมนตัมของจุดศูนย์กลางมวล
ซึ่งเป็นจุดที่เสมือนกับว่า มีมวลเท่ากับผลรวมของมวลทุกๆอนุภาคในระบบ
(
ทางด้านขวาของสมการที่ (5-15) คือผลรวมของโมเมนตัมสำหรับระบบซึ่งประกอบด้วย
n อนุภาค ซึ่งมีค่าเท่ากับโมเมนตัมของจุดศูนย์กลางมวล
ซึ่งเป็นจุดที่เสมือนกับว่า มีมวลเท่ากับผลรวมของมวลทุกๆอนุภาคในระบบ
(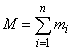 ) และมีความเร็วเป็น
) และมีความเร็วเป็น 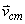
 ถ้าเราหาอนุพันธ์เทียบกับเวลาของสมการที่
(5-15) จะได้ ถ้าเราหาอนุพันธ์เทียบกับเวลาของสมการที่
(5-15) จะได้
 โดยที่ โดยที่
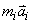 ที่ปรากฏทางด้านขวาของสมการที่ (5-16) (เมื่อพิจารณาตามกฏข้อที่สองของนิวตัน)
ก็คือ แรงที่กระทำต่ออนุภาค
ที่ปรากฏทางด้านขวาของสมการที่ (5-16) (เมื่อพิจารณาตามกฏข้อที่สองของนิวตัน)
ก็คือ แรงที่กระทำต่ออนุภาค 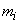 นั่นเอง นั่นเอง
 ดังนั้นค่าทั้งหมดที่ได้ทางด้านขวาของสมการดังกล่าว
คือผลรวมของแรงทั้งหมด ที่กระทำต่ออนุภาคในระบบ เนื่องจากแรงที่กระทำต่อนุภาค
ในระบบ อาจประกอบด้วยแรงภายใน (internal forces), ดังนั้นค่าทั้งหมดที่ได้ทางด้านขวาของสมการดังกล่าว
คือผลรวมของแรงทั้งหมด ที่กระทำต่ออนุภาคในระบบ เนื่องจากแรงที่กระทำต่อนุภาค
ในระบบ อาจประกอบด้วยแรงภายใน (internal forces), 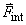 ,
และแรงภายนอก (external force), ,
และแรงภายนอก (external force), 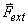 ,
แต่จากการพิจารณาแรง ที่มีผลต่อนุภาคในระบบ โดยอาศัยกฏข้อที่สามของนิวตันจะพบว่า
แรงภายใน ซึ่งเป็นแรงที่เกิดระหว่างอนุภาค จะมีการหักล้างกันหมดไป ,
แต่จากการพิจารณาแรง ที่มีผลต่อนุภาคในระบบ โดยอาศัยกฏข้อที่สามของนิวตันจะพบว่า
แรงภายใน ซึ่งเป็นแรงที่เกิดระหว่างอนุภาค จะมีการหักล้างกันหมดไป
 ดังนั้น
จึงเหลือเฉพาะแรงภายนอกเท่านั้น ที่กระทำต่ออนุภาคในระบบ
ดังนั้นสมการที่ (5-16) เขียนได้ใหม่เป็น ดังนั้น
จึงเหลือเฉพาะแรงภายนอกเท่านั้น ที่กระทำต่ออนุภาคในระบบ
ดังนั้นสมการที่ (5-16) เขียนได้ใหม่เป็น
 จากสมการที่
(5-17) จะเห็นว่าผลรวมของแรงภายนอกทั้งหมด จากสมการที่
(5-17) จะเห็นว่าผลรวมของแรงภายนอกทั้งหมด 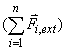 มีผลทำให้จุดศูนย์กลางมวลของระบบเคลื่อนที่ด้วยความเร่ง มีผลทำให้จุดศูนย์กลางมวลของระบบเคลื่อนที่ด้วยความเร่ง
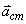
 จากสมการที่
(5-15), (5-16) และ (5-17) ข้างต้น แสดงให้เห็นว่า การเคลื่อนที่ของระบบอนุภาค
สามารถพิจารณาได้จากจุดศูนย์กลางมวล โดยเฉพาะอย่างยิ่งสมการที่
(5-17) แสดงให้เห็นว่า จุดศูนย์กลางมวลของระบบอนุภาค
จะเคลื่อนที่ด้วยความเร่งเสมือนกับว่ามันเป็นอนุภาคหนึ่ง
ที่มีมวลเท่ากับมวลทั้งหมดของระบบอนุภาค เมื่อมีแรงภายนอกมากระทำ
แต่ถ้าไม่มีแรงภายนอกมากระทำ จุดศูนย์กลางของระบบจะหยุดนิ่ง
หรือเคลื่อนที่ด้วยความเร็วคงตัว ตามสภาพที่เป็นอยู่เดิม จากสมการที่
(5-15), (5-16) และ (5-17) ข้างต้น แสดงให้เห็นว่า การเคลื่อนที่ของระบบอนุภาค
สามารถพิจารณาได้จากจุดศูนย์กลางมวล โดยเฉพาะอย่างยิ่งสมการที่
(5-17) แสดงให้เห็นว่า จุดศูนย์กลางมวลของระบบอนุภาค
จะเคลื่อนที่ด้วยความเร่งเสมือนกับว่ามันเป็นอนุภาคหนึ่ง
ที่มีมวลเท่ากับมวลทั้งหมดของระบบอนุภาค เมื่อมีแรงภายนอกมากระทำ
แต่ถ้าไม่มีแรงภายนอกมากระทำ จุดศูนย์กลางของระบบจะหยุดนิ่ง
หรือเคลื่อนที่ด้วยความเร็วคงตัว ตามสภาพที่เป็นอยู่เดิม
| |
 ตัวอย่างที่ 5-5 (TPhO1)
ตัวอย่างที่ 5-5 (TPhO1) |
 |
มวลเล็ก ๆ A และ B ผูกติดที่ปลายแต่ละข้างของสปริงเบาและยืดออกยาว
1.5 m มวลทั้งสองอยู่บนพื้นลื่นโดย A ห่างจากผนัง
1 m เมื่อปล่อยให้ระบบเคลื่อนที่ ถามว่าขณะสปริงหดลงเหลือความยาว
1.2 m นั้น A จะอยู่ห่างจากผนังเท่าไร
วิธีทำ
โจทย์ลักษณะนี้จะพบได้ทั่วไป และเป็นกรณีเดียวกับการไต่เชือก
ที่ห้อยจากบอลลูนที่ลอยนิ่ง การเดินบนเรือหรือแพ
หรือ การผลักกันของนักสเกตน้ำแข็ง ซึ่งทั้งหมดมีสิ่งหนึ่งร่วมกัน
คือ การไม่มีแรงภายนอกมากระทำ หรือ แรงลัพธ์ของแรงภายนอกทั้งหมดมีค่าเป็นศูนย์
ดังนั้น จากสมการที่ 5-17
จึงได้ว่า
นั่นคือจุดศูนย์กลางมวลไม่มีความเร่ง ซึ่งก็แสดงว่า
จุดศูนย์กลางมวล จะต้องเคลื่อนด้วยความเร็วคงที่
หรือ ว่าหยุดนิ่ง สำหรับในกรณีนี้เดิมมวลทั้งสองก้อนอยู่นิ่ง
จึงทำให้จุดศูนย์กลางมวลอยู่นิ่งไปด้วย
ใช้สมการการหาจุดศูนย์กลางมวลสำหรับระบบสองอนุภาค
สมการที่ 5-1 จะได้ว่า
เมื่อความยาวของสปริงเหลือ 1.2 m ตำแหน่งของจุดศูนย์กลางมวลไม่ได้เปลี่ยนไป
แต่ตำแหน่ง xA และ xB
เปลี่ยนไป การจะหาตำแหน่ง xA ทำได้โดยแทนค่าลงในสมการแสดงจุดศูนย์กลางมวลอีกครั้งหนึ่ง
ขณะสปริงหดลงเหลือความยาว 1.2 m นั้น A จะอยู่ห่างจากผนัง
1.1 m
|
|
 ตัวอย่างที่ 5-6
ตัวอย่างที่ 5-6 |
 |
ระบบอนุภาคซึ่งประกอบด้วย
อนุภาคมีมวล 4.0, 4.0 และ 8.0 kgตามตำแหน่งดังในกราฟ
จงหาความเร่งของจุดศูนย์กลาง 24 เมื่อมีแรงมากระทำดังรูป
วิธีทำ
จากสมการที่ 5-17 จะได้ว่า
|
|