การประยุกต์ใช้กฎข้อที่สองของนิวตัน กับการเคลื่อนที่แบบวงกลม
ในลักษณะไม่สม่ำเสมอ (อัตราเร็วไม่คงที่)
จากที่ได้ทราบถึงการเคลื่อนที่เป็นวงกลม
ในลักษณะที่อัตราเร็วเชิงมุมสม่ำเสมอ ซึ่งมีเฉพาะ
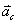
แต่ไม่มี
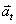
ไปแล้วนั้น
ในตอนนี้จะทำการพิจารณาการเคลื่อนที่เป็นวงกลม แต่เป็นลักษณะที่อัตราเร็วเชิงมุมมีค่าไม่สม่ำเสมอ
ความเร็วของการเคลื่อนที่แบบวงกลม ในลักษณะไม่สม่ำเสมอนั้น
มีการเปลี่ยนแปลงทั้งขนาดและทิศทาง ทำให้เกิดความเร่งทั้งสองแนว
ดังนั้นความเร่งรวมของวัตถุ
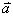
สำหรับการเคลื่อนที่เป็นวงกลมแบบไม่สม่ำเสมอ จะเป็นผลรวมระหว่าง
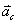
กับ
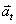
โดยที่
รูปที่ 2-8 ผลรวมของเวกเตอร์ลัพธ์ของแร งในกรณีของการเคลื่อนที่แบบวงกลมในลักษณะไม่สม่ำเสมอ |
ดังนั้นแรงที่กระทำต่อวัตถุ
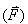
ในกรณีของการเคลื่อนที่เป็นวงกลมแบบไม่สม่ำเสมอ
จึงเป็นผลรวมของแรงในแนวสู่ศูนย์กลาง
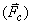
และแรงในแนวสัมผัส
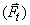
ตามรูปที่ 2-8
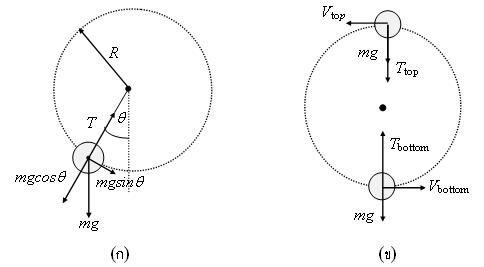
รูปที่ 2-9 การเคลื่อนที่เป็นวงกลมของลูกบอลในลักษณะไม่สม่ำเสมอ |
| (ก) แสดงแรงที่กระทำต่อลูกบอลมวล m
ซึ่งประกอบด้วยแรงตึงเชือก T และ น้ำหนัก
mg |
| (ข) แสดงแรงที่กระทำต่อลูกบอลมวล m เมื่อลูกบอลอยู่ที่จุดสูงสุดและต่ำสุด |
|
ตัวอย่างหนึ่งที่น่าสนใจ
เช่น มีลูกบอลมวล m ผูกติดไว้กับเชือกเบายาว R (รูปที่
2-9) ถ้าลูกบอลถูกแกว่งให้เคลื่อนที่เป็นวงกลม โดยมีระนาบของการแกว่งอยู่ในแนวดิ่ง
จากการวิเคราะห์พบว่าแรงตึงเชือกเมื่อลูกบอลอยู่ที่จุดสูงสุดจะมีค่าน้อยที่สุด
แต่ถ้าลูกบอลอยู่ที่ตำแหน่งต่ำสุด ค่าของแรงตึงเชือกจะมีค่ามากที่สุด
รูปที่
2-9 (ก) แสดงแรงทั้งหมดที่กระทำต่อลูกบอลมวล m ซึ่งประกอบด้วยแรงตึงในเส้นเชือก
และน้ำหนัก
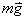
เมื่อพิจารณาขณะที่เชือกทำมุม
θ กับแนวดิ่ง และอาศัยกฎข้อที่สองของนิวตัน แรงในแนวสัมผัสเขียนได้เป็น
ซึ่งแรงในแนวเส้นสัมผัสนี้ทำให้วัตถุมีความเร็วในแนวเส้นสัมผัสเปลี่ยนไป
ส่วนแรงในแนวรัศมี
(แรงสู่ศูนย์กลาง) สามารถเขียนได้เป็น
เมื่อพิจารณาสมการที่
(2-14) พบว่า ณ จุดสูงสุด
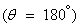
ซึ่งเป็นแรงตึงเชือกที่มีค่าต่ำสุด
นอกจากนี้เมื่อพิจารณาสมการที่ (2-13) จะพบอีกว่า ณ
จุดสูงสุด ความเร่งในแนวสัมผัสเป็นศูนย์
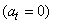
ดังนั้น วัตถุจึงมีความเร่ง เฉพาะในแนวสู่ศูนย์กลางเท่านั้น
และเมื่อพิจารณาสมการที่ (2-14) ณ จุดต่ำสุด
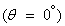
ซึ่งเป็นแรงตึงเชือกที่มีค่าสูงสุด
และก็เช่นเดียวกัน ที่จุดต่ำสุด ความเร่งในแนวเส้นสัมผัสเป็นศูนย์
วัตถุจึงมีความเร่งเฉพาะในแนวสู่ศูนย์กลางเท่านั้น (รูปที่
2-9 (ข))
