 สมการของความต่อเนื่อง (the equation of continuity)
สมการของความต่อเนื่อง (the equation of continuity) |
|
 มวลของของไหลจะไม่เปลี่ยนแปลงในขณะที่มันเคลื่อนที่
นี่เป็นที่มา ของสมการของความต่อเนื่อง พิจารณาส่วนหนึ่งของ flow tube
ที่อยู่ระหว่างภาคตัดขวาง 2 บริเวณ ดังแสดงในรูปที่ 8-6 ของไหลกำลังเคลื่อนที่จากด้านล่างไปยังด้านบนของ
flow tube ภาคตัดขวางด้านล่างมีพื้นที่ A1 และด้านบนมีพื้นที่
A2 อัตราเร็วของของไหลที่บริเวณทั้งสองนี้มีค่าเป็น v1
และ v2 ตามลำดับ ไม่มีของไหลผ่านเข้าออกระหว่างผนังของ
flow tube นี้ เนื่องจากที่ทุกจุดบนผนังของ flow tube เวกเตอร์ความเร็วของของไหลจะขนานกับผนัง
ในช่วงระยะเวลาสั้น ๆ dt ของไหลจากพื้นที่หน้าตัด A1 จะเคลื่อนที่ได้ระยะทาง
v1dt ดังนั้น จะได้ของไหลรูปท่อทรงกระบอกที่มีความสูง v1dt
พื้นที่หน้าตัด A1 และมีปริมาตรเป็น มวลของของไหลจะไม่เปลี่ยนแปลงในขณะที่มันเคลื่อนที่
นี่เป็นที่มา ของสมการของความต่อเนื่อง พิจารณาส่วนหนึ่งของ flow tube
ที่อยู่ระหว่างภาคตัดขวาง 2 บริเวณ ดังแสดงในรูปที่ 8-6 ของไหลกำลังเคลื่อนที่จากด้านล่างไปยังด้านบนของ
flow tube ภาคตัดขวางด้านล่างมีพื้นที่ A1 และด้านบนมีพื้นที่
A2 อัตราเร็วของของไหลที่บริเวณทั้งสองนี้มีค่าเป็น v1
และ v2 ตามลำดับ ไม่มีของไหลผ่านเข้าออกระหว่างผนังของ
flow tube นี้ เนื่องจากที่ทุกจุดบนผนังของ flow tube เวกเตอร์ความเร็วของของไหลจะขนานกับผนัง
ในช่วงระยะเวลาสั้น ๆ dt ของไหลจากพื้นที่หน้าตัด A1 จะเคลื่อนที่ได้ระยะทาง
v1dt ดังนั้น จะได้ของไหลรูปท่อทรงกระบอกที่มีความสูง v1dt
พื้นที่หน้าตัด A1 และมีปริมาตรเป็น 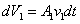 ซึ่งกำลังไหลเข้าไปใน flow tube ผ่านพื้นที่หน้าตัด A1
ซึ่งกำลังไหลเข้าไปใน flow tube ผ่านพื้นที่หน้าตัด A1
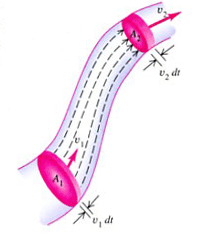
รูปที่ 9-6 ส่วนหนึ่งของ flow tube ของของไหลที่กำลังไหล |
 ในช่วงเวลาสั้น
ๆ เดียวกันนี้ ของไหลรูปท่อทรงกระบอกที่มีปริมาตรเป็น ในช่วงเวลาสั้น
ๆ เดียวกันนี้ ของไหลรูปท่อทรงกระบอกที่มีปริมาตรเป็น 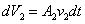 ก็กำลังไหลออกจาก
flow tube ผ่านพื้นที่หน้าตัด A2 ก็กำลังไหลออกจาก
flow tube ผ่านพื้นที่หน้าตัด A2
 เราจะพิจารณาสำหรับกรณีของของไหลที่บีบอัดไม่ได้
นั่นคือความหนาแน่น เราจะพิจารณาสำหรับกรณีของของไหลที่บีบอัดไม่ได้
นั่นคือความหนาแน่น 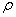 มีค่าคงที่ที่ทุกจุด
มวล มีค่าคงที่ที่ทุกจุด
มวล 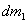 ของของไหลรูปท่อทรงกระบอกที่กำลังไหลเข้าไปใน
flow tube ผ่านพื้นที่หน้าตัด A1 ในช่วงเวลา dt คือ ของของไหลรูปท่อทรงกระบอกที่กำลังไหลเข้าไปใน
flow tube ผ่านพื้นที่หน้าตัด A1 ในช่วงเวลา dt คือ 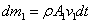 เช่นเดียวกันสำหรับมวล เช่นเดียวกันสำหรับมวล
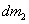 ของของไหล
รูปท่อทรงกระบอก ที่กำลังไหลออกจาก flow tube ผ่านพื้นที่หน้าตัด A2
จะได้ ของของไหล
รูปท่อทรงกระบอก ที่กำลังไหลออกจาก flow tube ผ่านพื้นที่หน้าตัด A2
จะได้ 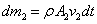 ใน
steady flow มวลรวมภายใน flow tube ต้องมีค่าคงที่ นั่นคือ ใน
steady flow มวลรวมภายใน flow tube ต้องมีค่าคงที่ นั่นคือ 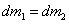 จะได้ว่า จะได้ว่า
|
|
หรือ 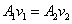
|
(8-1) |
 สมการ
(8-1) นี้เป็น สมการของความต่อเนื่อง (continuity equation) สำหรับของไหลที่บีบอัดไม่ได้
ผลคูณ สมการ
(8-1) นี้เป็น สมการของความต่อเนื่อง (continuity equation) สำหรับของไหลที่บีบอัดไม่ได้
ผลคูณ 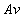 คือ
อัตราการไหลเชิงปริมาตร (volume flow rate) คือ
อัตราการไหลเชิงปริมาตร (volume flow rate) 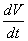 (หรืออาจเรียกสั้น ๆ ว่า อัตราการไหล) ซึ่งคือปริมาตรของของไหลที่ไหลผ่านพื้นที่ตัดขวางหนึ่งของ
flow tube ในหนึ่งหน่วยเวลา
(หรืออาจเรียกสั้น ๆ ว่า อัตราการไหล) ซึ่งคือปริมาตรของของไหลที่ไหลผ่านพื้นที่ตัดขวางหนึ่งของ
flow tube ในหนึ่งหน่วยเวลา
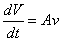
(volume flow rate) |
(8-2) |
 เราอาจวัดอัตราการไหลของของไหลโดยใช้
อัตราการไหลเชิงมวล (mass flow rate) ซึ่งหมายถึงมวลของของไหลที่ไหลผ่านพื้นที่ตัดขวางหนึ่งในของ
flow tube ในหนึ่งหน่วยเวลา เราสามารถคำนวณได้โดยคูณ เราอาจวัดอัตราการไหลของของไหลโดยใช้
อัตราการไหลเชิงมวล (mass flow rate) ซึ่งหมายถึงมวลของของไหลที่ไหลผ่านพื้นที่ตัดขวางหนึ่งในของ
flow tube ในหนึ่งหน่วยเวลา เราสามารถคำนวณได้โดยคูณ 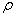 ด้วยความหนาแน่นของของไหล ด้วยความหนาแน่นของของไหล
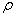 ดังนี้ ดังนี้
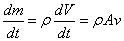
(mass flow rate) |
(8-3) |
 สมการของความต่อเนื่อง สมการของความต่อเนื่อง
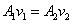 แสดงให้เห็นว่าอัตราการไหลมีค่าคงที่ที่ทุกจุดใน flow tube เมื่อพื้นที่หน้าตัดของ
flow tube มีขนาดลดลง ของไหลจะไหลได้เร็วขึ้น (อัตราเร็วของของไหลมากขึ้น)
และในทางกลับกัน เมื่อพื้นที่หน้าตัดของ flow tube มีขนาดเพิ่มขึ้น ของไหลจะไหลได้ช้าลง
(อัตราเร็วของของไหลน้อยลง) ตัวอย่างที่มีให้เห็นในธรรมชาติคืออัตราเร็วของน้ำในแม่น้ำ
ในบริเวณที่ลึกพื้นที่หน้าตัดของแม่น้ำมีขนาดใหญ่ จึงทำให้กระแสน้ำไหลได้ช้ากว่าในบริเวณที่ตื้นกว่าซึ่งมีพื้นที่หน้าตัดเล็กกว่า
อีกตัวอย่างหนึ่งคือถ้าเราสังเกตการไหลของน้ำที่ออกมาจากก๊อก เราจะเห็นว่าลำของน้ำจะแคบลงเนื่องจากมันตกลงมาเร็วขึ้น
ทั้งนี้ก็เพราะอัตราการไหล
แสดงให้เห็นว่าอัตราการไหลมีค่าคงที่ที่ทุกจุดใน flow tube เมื่อพื้นที่หน้าตัดของ
flow tube มีขนาดลดลง ของไหลจะไหลได้เร็วขึ้น (อัตราเร็วของของไหลมากขึ้น)
และในทางกลับกัน เมื่อพื้นที่หน้าตัดของ flow tube มีขนาดเพิ่มขึ้น ของไหลจะไหลได้ช้าลง
(อัตราเร็วของของไหลน้อยลง) ตัวอย่างที่มีให้เห็นในธรรมชาติคืออัตราเร็วของน้ำในแม่น้ำ
ในบริเวณที่ลึกพื้นที่หน้าตัดของแม่น้ำมีขนาดใหญ่ จึงทำให้กระแสน้ำไหลได้ช้ากว่าในบริเวณที่ตื้นกว่าซึ่งมีพื้นที่หน้าตัดเล็กกว่า
อีกตัวอย่างหนึ่งคือถ้าเราสังเกตการไหลของน้ำที่ออกมาจากก๊อก เราจะเห็นว่าลำของน้ำจะแคบลงเนื่องจากมันตกลงมาเร็วขึ้น
ทั้งนี้ก็เพราะอัตราการไหล 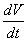 คงที่ที่ทุกจุดของลำน้ำ
ถ้ามีน้ำไหลจากท่อน้ำที่มีขนาดเส้นผ่านศูนย์กลาง 2 เซนติเมตรไปยังอีกท่อหนึ่งที่ต่อกันอยู่ซึ่งมีขนาดเส้นผ่านศูนย์กลาง
1 เซนติเมตร อัตราเร็วของการไหล (flow speed: v) จะเพิ่มขึ้นเป็น 4 เท่าเมื่อมันอยู่ในท่อที่สอง คงที่ที่ทุกจุดของลำน้ำ
ถ้ามีน้ำไหลจากท่อน้ำที่มีขนาดเส้นผ่านศูนย์กลาง 2 เซนติเมตรไปยังอีกท่อหนึ่งที่ต่อกันอยู่ซึ่งมีขนาดเส้นผ่านศูนย์กลาง
1 เซนติเมตร อัตราเร็วของการไหล (flow speed: v) จะเพิ่มขึ้นเป็น 4 เท่าเมื่อมันอยู่ในท่อที่สอง
 สำหรับของไหลที่บีบอัดได้
นั่นคือความหนาแน่นของของไหลไม่เท่ากันที่ตำแหน่งต่าง ๆ กัน ถ้า สำหรับของไหลที่บีบอัดได้
นั่นคือความหนาแน่นของของไหลไม่เท่ากันที่ตำแหน่งต่าง ๆ กัน ถ้า 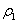 และ และ
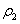 คือความหนาแน่นของของไหลที่บริเวณที่
1 และ 2 ตามลำดับ เราต้องใช้ความสัมพันธ์ คือความหนาแน่นของของไหลที่บริเวณที่
1 และ 2 ตามลำดับ เราต้องใช้ความสัมพันธ์
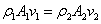
(continuity equation, compressible fluid) |
(8-4) |
UP
 |
|















