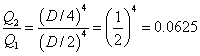หัวข้อที่จะได้ศึกษา


  

กฎของปัวซอยย์ (Poiseuille’s law)

เราจะพิจารณาอัตราการไหลของของไหลในท่อทรงกระบอกที่มีพื้นที่หน้าตัดคงที่ ดูรูปที่ 8-11 กำหนดให้การไหลภายในท่อเป็นแบบ laminar flow และของไหลมีความหนืดค่าหนึ่ง เราจะพบว่าอัตราเร็วของการไหลมีค่ามากที่สุดที่ตรงกลางท่อและอัตราเร็วเป็นศูนย์ที่ผนังท่อ


รูปที่ 8-11 ของไหลที่มีความหนืดกำลังไหลในท่อทรงกระบอกที่มีพื้นที่หน้าตัดคงที่

โดยใช้สมการ (8-14) ที่แสดงนิยามของความหนืด กับส่วนของของไหลรูปท่อทรงกระบอกนี้ เราจะได้สมการที่บรรยายอัตราเร็วของการไหลที่ตำแหน่งต่าง ๆ บนหน้าตัดของทรงกระบอก เราจะไม่ดูในรายละเอียดที่มาของสมการ อัตราเร็วของการไหล v ที่ระยะ r จากแกนกลางของท่อที่มีรัศมี R คือ
(8-16)

เมื่อ p1 และ p1 คือความดันที่ปลายทั้งสองของท่อยาว L จะเห็นว่าอัตราเร็วที่จุดใด ๆ แปรผันตรงกับผลต่างความดันต่อหน่วยความยาว หรือ ซึ่งเรียกว่า pressure gradient (การไหลจะเกิดในทิศทางที่ความดันลดลงเสมอ)

เพื่อหาอัตราการไหล (volume flow rate) ในท่อ เราจะพิจารณาวงแหวนเล็ก ๆ ที่มีรัศมีภายใน r รัศมีภายนอก และพื้นที่หน้าตัด อัตราการไหลของของไหลผ่านวงแหวนนี้จะมีค่าเป็น อัตราการไหลรวมทั้งหมดหาได้จากการอินทริเกตค่านี้จาก ไปยัง ผลที่ได้คือ

(8-17)

สมการนี้ถูกค้นพบครั้งแรกโดย Poiseuille จึงได้เรียกว่าสมการของปัวซอยย์ (Poiseuille’s equation) จะเห็นว่าอัตราการไหลแปรผกผันกับความหนืดตามที่คาด และเช่นเดียวกับอัตราเร็วของการไหล อัตราการไหลก็แปรผันตาม pressure gradient ด้วย และอัตราการไหลยังแปรผันตามกำลังสี่ของรัศมีของท่อ R4 ดังนั้นถ้าเราเพิ่ม R ขึ้นเป็น 2 เท่า อัตราการไหลก็จะเพิ่มขึ้น 16 เท่า ขนาดรัศมีของท่อ มีผลต่ออัตราการไหลมากกว่าผลต่างความดันหรือความยาวของท่อ
ตัวอย่างที่ 8-5
         เส้นโลหิตแดงใหญ่เส้นหนึ่ง มีขนาดเส้นผ่านศูนย์กลางภายในลดลงครึ่งหนึ่ง เนื่องจากมีสิ่งเกาะที่ผนังด้านใน ถ้าผลต่างความดันคร่อมเส้นเลือดมีค่าคงเดิม อัตราการไหลของเลือดผ่านเส้นเลือดที่บริเวณนี้จะลดลงด้วยอัตราส่วนเท่าไร

         วิธีทำ
         จากสมการของปัวซอยย์
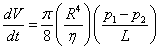
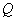
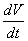
         ให้ แทน จะได้ว่า
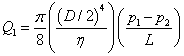
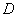
         เมื่อ คือเส้นผ่านศูนย์กลางของเส้นเลือดปกติ
         และเมื่อเส้นเลือดมีสิ่งกีดขวาง จะได้

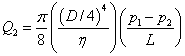
         ดังนั้น

           

UP