 สมการของแบร์นูลลี (Bernoullis equation)
สมการของแบร์นูลลี (Bernoullis equation) |
|
 จากสมการของความต่อเนื่อง
อัตราเร็วของการไหล สามารถเปลี่ยนแปลง ได้ตามเส้นทางการไหล ความดันก็สามารถเปลี่ยนแปลงได้เช่นกัน
ทั้งนี้ขึ้นอยู่กับความสูง (หรือความลึก) เช่นเดียวกันกับในของไหลสถิต
และความดันก็ขึ้นอยู่กับอัตราเร็วของการไหลด้วย เราจะหาความสัมพันธ์ระหว่างความดัน
อัตราเร็วของการไหลและความสูง สำหรับของไหลอุดมคติที่บีบอัดไม่ได้
(ideal and incompressible fluid) และการไหลเป็นแบบ steady flow จากสมการของความต่อเนื่อง
อัตราเร็วของการไหล สามารถเปลี่ยนแปลง ได้ตามเส้นทางการไหล ความดันก็สามารถเปลี่ยนแปลงได้เช่นกัน
ทั้งนี้ขึ้นอยู่กับความสูง (หรือความลึก) เช่นเดียวกันกับในของไหลสถิต
และความดันก็ขึ้นอยู่กับอัตราเร็วของการไหลด้วย เราจะหาความสัมพันธ์ระหว่างความดัน
อัตราเร็วของการไหลและความสูง สำหรับของไหลอุดมคติที่บีบอัดไม่ได้
(ideal and incompressible fluid) และการไหลเป็นแบบ steady flow
 จากสมการของความต่อเนื่อง
เมื่อมีของไหลที่บีบอัดไม่ได้ไหลอยู่ภายในท่อ ซึ่งมีขนาดของพื้นที่หน้าตัดแต่ละบริเวณเปลี่ยนแปลงไป
อัตราเร็วของการไหล ก็จะเปลี่ยนแปลงไปด้วย นั่นคือแต่ละส่วนของของไหลจ
ะต้องมีความเร่ง หรือความหน่วง แล้วแต่กรณี ของไหลที่อยู่รอบ ๆ ออกแรงกระทำให้เกิดความเร่งนี้
นั่นหมายความว่า ความดันจะต้องมีค่าต่างกันที่ตำแหน่งต่าง ๆ กัน เพราะถ้าความดันเท่ากันหมดทุกที่
แรงสุทธิที่กระทำกับทุก ๆ ส่วนของของไหลจะเป็นศูนย์ ทำให้ไม่เกิดความเร่ง
หรืออัตราเร็วจะคงที่ที่ทุกจุดซึ่งขัดแย้งกับข้างต้น เมื่อของไหลส่วนหนึ่งมีอัตราเร็วเพิ่มขึ้น
คือไหลเร็วขึ้น มันจะต้องเคลื่อนที่ มาจากบริเวณที่มีความดันมากกว่า
มายังบริเวณที่มีความดันน้อยกว่า เพื่อที่จะทำให้มีแรงสุทธิขนาดหนึ่งในการเร่งมัน
สรุปได้ว่าเมื่อพื้นที่หน้าตัดของ flow tube มีการเปลี่ยนขนาด ความดันจะต้องมีค่าเปลี่ยนไปด้วยถึงแม้ว่าทั้งสองบริเวณจะอยู่ที่ระดับสูงเดียวกัน
ถ้ามันอยู่คนระดับก็จะยิ่งช่วยเพิ่มความแตกต่างระหว่างความดันที่สองบริเวณ จากสมการของความต่อเนื่อง
เมื่อมีของไหลที่บีบอัดไม่ได้ไหลอยู่ภายในท่อ ซึ่งมีขนาดของพื้นที่หน้าตัดแต่ละบริเวณเปลี่ยนแปลงไป
อัตราเร็วของการไหล ก็จะเปลี่ยนแปลงไปด้วย นั่นคือแต่ละส่วนของของไหลจ
ะต้องมีความเร่ง หรือความหน่วง แล้วแต่กรณี ของไหลที่อยู่รอบ ๆ ออกแรงกระทำให้เกิดความเร่งนี้
นั่นหมายความว่า ความดันจะต้องมีค่าต่างกันที่ตำแหน่งต่าง ๆ กัน เพราะถ้าความดันเท่ากันหมดทุกที่
แรงสุทธิที่กระทำกับทุก ๆ ส่วนของของไหลจะเป็นศูนย์ ทำให้ไม่เกิดความเร่ง
หรืออัตราเร็วจะคงที่ที่ทุกจุดซึ่งขัดแย้งกับข้างต้น เมื่อของไหลส่วนหนึ่งมีอัตราเร็วเพิ่มขึ้น
คือไหลเร็วขึ้น มันจะต้องเคลื่อนที่ มาจากบริเวณที่มีความดันมากกว่า
มายังบริเวณที่มีความดันน้อยกว่า เพื่อที่จะทำให้มีแรงสุทธิขนาดหนึ่งในการเร่งมัน
สรุปได้ว่าเมื่อพื้นที่หน้าตัดของ flow tube มีการเปลี่ยนขนาด ความดันจะต้องมีค่าเปลี่ยนไปด้วยถึงแม้ว่าทั้งสองบริเวณจะอยู่ที่ระดับสูงเดียวกัน
ถ้ามันอยู่คนระดับก็จะยิ่งช่วยเพิ่มความแตกต่างระหว่างความดันที่สองบริเวณ
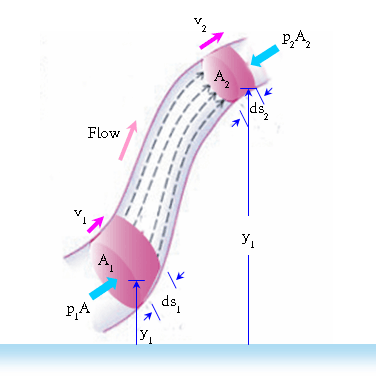
รูปที่ 8-7 ส่วนหนึ่งของ flow tube ของของไหลที่กำลังไหล |
 ต่อไปเราจะแสดงที่มาของสมการของแบร์นูลลี
โดยใช้ทฤษฎีของงานและพลังงาน ในการพิจารณาของไหลที่กำลังไหลใน flow tube
ดังรูปที่ 8-7 ของไหลกำลังไหลจากบริเวณที่ 1 ไปยังบริเวณที่ 2 ที่อยู่สูงกว่า
อัตราเร็วของการไหลที่บริเวณที่ 1 และ 2 คือ v1 และ v2
ตามลำดับ ในช่วงระยะเวลาสั้น ๆ dt ของไหลที่บริเวณที่ 1 เคลื่อนที่ขึ้นได้ระยะทาง ต่อไปเราจะแสดงที่มาของสมการของแบร์นูลลี
โดยใช้ทฤษฎีของงานและพลังงาน ในการพิจารณาของไหลที่กำลังไหลใน flow tube
ดังรูปที่ 8-7 ของไหลกำลังไหลจากบริเวณที่ 1 ไปยังบริเวณที่ 2 ที่อยู่สูงกว่า
อัตราเร็วของการไหลที่บริเวณที่ 1 และ 2 คือ v1 และ v2
ตามลำดับ ในช่วงระยะเวลาสั้น ๆ dt ของไหลที่บริเวณที่ 1 เคลื่อนที่ขึ้นได้ระยะทาง
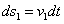 และของไหลที่บริเวณที่ 2 เคลื่อนที่ขึ้นได้ระยะทาง
และของไหลที่บริเวณที่ 2 เคลื่อนที่ขึ้นได้ระยะทาง 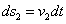 ถ้าพื้นที่หน้าตัดที่บริเวณที่ 1 และ 2 คือ A1 และ A2
ตามลำดับ จากสมการของความต่อเนื่อง เราจะได้ว่าสำหรับของไหลที่บีบอัดไม่ได้
(ความหนาแน่นคงที่) ปริมาตรของของไหล dV ที่ไหลผ่านพื้นที่หน้าตัดใด
ๆ ในช่วงเวลา dt (อัตราการไหล) จะมีค่าคงที่ นั่นคือ
ถ้าพื้นที่หน้าตัดที่บริเวณที่ 1 และ 2 คือ A1 และ A2
ตามลำดับ จากสมการของความต่อเนื่อง เราจะได้ว่าสำหรับของไหลที่บีบอัดไม่ได้
(ความหนาแน่นคงที่) ปริมาตรของของไหล dV ที่ไหลผ่านพื้นที่หน้าตัดใด
ๆ ในช่วงเวลา dt (อัตราการไหล) จะมีค่าคงที่ นั่นคือ
 พิจารณางานที่ทำบนส่วนของของไหลนี้ในช่วงระยะเวลา
dt ถ้าความดันที่บริเวณที่ 1 และ 2 คือ p 1 และ p2
ตามลำดับ แรงที่ทำบนพื้นที่หน้าตัดของบริเวณที่ 1 คือ p1A1 และที่บริเวณที่
2 คือ p2A2 ดังนั้นงานสุทธิ dW ที่ทำบนส่วนของของไหล
เมื่อของไหลเคลื่อนที่คือ พิจารณางานที่ทำบนส่วนของของไหลนี้ในช่วงระยะเวลา
dt ถ้าความดันที่บริเวณที่ 1 และ 2 คือ p 1 และ p2
ตามลำดับ แรงที่ทำบนพื้นที่หน้าตัดของบริเวณที่ 1 คือ p1A1 และที่บริเวณที่
2 คือ p2A2 ดังนั้นงานสุทธิ dW ที่ทำบนส่วนของของไหล
เมื่อของไหลเคลื่อนที่คือ
 เทอมที่สองของสมการ
(8-6) นี้มีเครื่องหมายเป็นลบเนื่องจากแรงที่ทำที่บริเวณที่ 2 มีทิศตรงข้ามกับทิศของการเคลื่อนที่ของของไหล
(ของไหลพยายามเคลื่อนที่ ต้านความดันเนื่องจากของไหลด้านขวาที่บริเวณที่
2) เทอมที่สองของสมการ
(8-6) นี้มีเครื่องหมายเป็นลบเนื่องจากแรงที่ทำที่บริเวณที่ 2 มีทิศตรงข้ามกับทิศของการเคลื่อนที่ของของไหล
(ของไหลพยายามเคลื่อนที่ ต้านความดันเนื่องจากของไหลด้านขวาที่บริเวณที่
2)
 งานที่ทำ
dW จะเท่ากับพลังงานกลสุทธิที่เปลี่ยนไป โดยที่พลังงานกลสุทธิ คือผลรวมของพลังงานจลน์กับพลังงานศักย์เนื่องจากแรงโน้มถ่วง
พิจารณาที่บริเวณที่ 1 ปริมาตรของของไหล ที่เคลื่อนที่ภายในช่วงเวลา
dt คือ งานที่ทำ
dW จะเท่ากับพลังงานกลสุทธิที่เปลี่ยนไป โดยที่พลังงานกลสุทธิ คือผลรวมของพลังงานจลน์กับพลังงานศักย์เนื่องจากแรงโน้มถ่วง
พิจารณาที่บริเวณที่ 1 ปริมาตรของของไหล ที่เคลื่อนที่ภายในช่วงเวลา
dt คือ 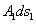 นั่นหมายถึงมวลของของไหลปริมาตรนี้คือ นั่นหมายถึงมวลของของไหลปริมาตรนี้คือ
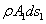 ดังนั้นมันมีพลังงานจลน์เท่ากับ ดังนั้นมันมีพลังงานจลน์เท่ากับ
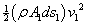 ในทำนองเดียวกัน
ที่บริเวณที่ 2 ของไหลในส่วนนั้นมีพลังงานจลน์เท่ากับ ในทำนองเดียวกัน
ที่บริเวณที่ 2 ของไหลในส่วนนั้นมีพลังงานจลน์เท่ากับ 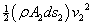 ดังนั้นพลังงานจลน์สุทธิที่เปลี่ยนไปมีค่าเป็น ดังนั้นพลังงานจลน์สุทธิที่เปลี่ยนไปมีค่าเป็น
 คราวนี้พิจารณาพลังงานศักย์
ที่บริเวณที่ 1 พลังงานศักย์เนื่องจากแรงโน้มถ่วงมีค่าเป็น คราวนี้พิจารณาพลังงานศักย์
ที่บริเวณที่ 1 พลังงานศักย์เนื่องจากแรงโน้มถ่วงมีค่าเป็น 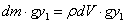 และที่บริเวณที่สองมีค่าเป็น และที่บริเวณที่สองมีค่าเป็น
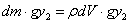 ดังนั้นพลังงานศักย์เนื่องจากแรงโน้มถ่วงที่เปลี่ยนไปคือ ดังนั้นพลังงานศักย์เนื่องจากแรงโน้มถ่วงที่เปลี่ยนไปคือ
 เนื่องจากงานที่ทำ เนื่องจากงานที่ทำ
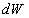 จะเท่ากับพลังงานกลสุทธิที่เปลี่ยนไป
นั่นคือ จะเท่ากับพลังงานกลสุทธิที่เปลี่ยนไป
นั่นคือ 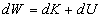 เราจะได้ว่า เราจะได้ว่า
|
(8-9) |
หรือ 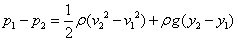 |
(8-10) |
 สมการ
(8-10) นี้คือ สมการของแบร์นูลลี (Bernoullis equation) สมการนี้อธิบายว่า
งานที่ทำบนปริมาตรหนึ่งหน่วยของของไหล โดยของไหลรอบ ๆ จะเท่ากับผลรวมของพลังงานจลน์
ที่เปลี่ยนไปกับพลังงานศักย์ที่เปลี่ยนไป ต่อหนึ่งหน่วยปริมาตรซึ่งเกิดขึ้นระหว่างการไหล
เราอาจแปลสมการของแบร์นูลล ีในรูปของความดันก็ได้ เทอมแรกของสมการด้านขวาคือ
ผลต่างความดันที่เกี่ยวข้องกับการเปลี่ยนแปลงของอัตราเร็วของการไหล เทอมที่สองคือ
ผลต่างความดันที่เกิดจากน้ำหนักของของไหล กับผลต่างความสูงที่สองบริเวณ
เราอาจเขียนสมการ (8-10) ใหม่ให้อยู่ในรูปที่ดูสะดวกกว่าดังนี้ สมการ
(8-10) นี้คือ สมการของแบร์นูลลี (Bernoullis equation) สมการนี้อธิบายว่า
งานที่ทำบนปริมาตรหนึ่งหน่วยของของไหล โดยของไหลรอบ ๆ จะเท่ากับผลรวมของพลังงานจลน์
ที่เปลี่ยนไปกับพลังงานศักย์ที่เปลี่ยนไป ต่อหนึ่งหน่วยปริมาตรซึ่งเกิดขึ้นระหว่างการไหล
เราอาจแปลสมการของแบร์นูลล ีในรูปของความดันก็ได้ เทอมแรกของสมการด้านขวาคือ
ผลต่างความดันที่เกี่ยวข้องกับการเปลี่ยนแปลงของอัตราเร็วของการไหล เทอมที่สองคือ
ผลต่างความดันที่เกิดจากน้ำหนักของของไหล กับผลต่างความสูงที่สองบริเวณ
เราอาจเขียนสมการ (8-10) ใหม่ให้อยู่ในรูปที่ดูสะดวกกว่าดังนี้
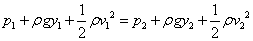 (Bernoullis
equation) |
(8-11) |
 ตัวห้อยเลข
1 และ 2 แทนตำแหน่งสองตำแหน่งใด ๆ ใน flow tube ดังนั้นเราสามารถเขียนได้ว่า ตัวห้อยเลข
1 และ 2 แทนตำแหน่งสองตำแหน่งใด ๆ ใน flow tube ดังนั้นเราสามารถเขียนได้ว่า
 สมการของแบร์นูลลีมีประโยชน์มากในการแก้ปัญหาการไหลในลักษณะต่าง
ๆ เช่นเพื่อที่จะคำนวณหาความดัน หรืออัตราเร็วของการไหลที่บริเวณต่าง
ๆ ในลำของของไหลหนึ่ง ๆ แต่ต้องระลึกไว้ว่าสมการของแบร์นูลลีใช้ได้เฉพาะกับของไหลอุดมคติที่บีบอัดไม่ได้
และไหลแบบ steady flow เท่านั้น ตัวอย่างต่อไปนี้แสดงให้เห็นถึงการแก้ปัญหาบางปัญหาโดยใช้สมการของแบร์นูลลี สมการของแบร์นูลลีมีประโยชน์มากในการแก้ปัญหาการไหลในลักษณะต่าง
ๆ เช่นเพื่อที่จะคำนวณหาความดัน หรืออัตราเร็วของการไหลที่บริเวณต่าง
ๆ ในลำของของไหลหนึ่ง ๆ แต่ต้องระลึกไว้ว่าสมการของแบร์นูลลีใช้ได้เฉพาะกับของไหลอุดมคติที่บีบอัดไม่ได้
และไหลแบบ steady flow เท่านั้น ตัวอย่างต่อไปนี้แสดงให้เห็นถึงการแก้ปัญหาบางปัญหาโดยใช้สมการของแบร์นูลลี
UP
 |
| |
 ตัวอย่างที่ 8-1 Static Fluids
ตัวอย่างที่ 8-1 Static Fluids |
| |
สังเกตว่าเมื่อของไหลไม่มีการเคลื่อนที่ 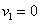 และ
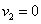 ดังนั้นสมการของแบร์นูลลีจะลดรูปลงเป็น
|
| |
 ตัวอย่างที่ 8-2 ความดันของของไหลที่ไหลในท่อที่มีพื้นที่หน้าตัดคงที่
ตัวอย่างที่ 8-2 ความดันของของไหลที่ไหลในท่อที่มีพื้นที่หน้าตัดคงที่ |
| |
|
| |
 ตัวอย่างที่ 8-3 Horizontal Pipe
ตัวอย่างที่ 8-3 Horizontal Pipe |
| |
| |
| |
 ตัวอย่างที่ 8-4 Efflux Speed่
ตัวอย่างที่ 8-4 Efflux Speed่ |
| |
ถังน้ำในรูปบรรจุน้ำไว้ตอนเริ่มต้น ข้าง ๆ ถังน้ำมีท่อเล็ก
ๆ ต่ออยู่ซึ่งอยู่ต่ำจากผิวน้ำในถังเป็นระยะ h ถ้าถังนี้มีฝาปิดอยู่และความดันอากาศภายในบริเวณเหนือผิวน้ำในถังคือ
p0 เราต้องการคำนวณหาอัตราเร็วของการไหลของน้ำออกจากท่อ
เราสมมุติว่าน้ำเป็นของไหลอุดมคติและบีบอัดไม่ได้
ดังนั้นเราสามารถใช้สมการของแบร์นูลลีในการศึกษาปัญหาการไหลของน้ำนี้ได้
กำหนดจุดที่ 1 และ 2 ดังรูป จะได้ |
|
|
เมื่อความดันที่จุดที่ 1 คือความดันบรรยากาศ
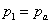 และความดันที่จุดที่
2 คือ และความดันที่จุดที่
2 คือ 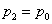 เราจะได้ว่า เราจะได้ว่า
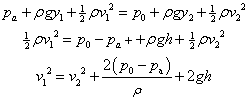
|
 จากสมการของความต่อเนื่อง
ถ้าพื้นที่หน้าตัดของท่อน้ำออก จากสมการของความต่อเนื่อง
ถ้าพื้นที่หน้าตัดของท่อน้ำออก 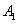 มีขนาดน้อยกว่าพื้นที่หน้าตัดของถังน้ำ มีขนาดน้อยกว่าพื้นที่หน้าตัดของถังน้ำ
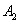 มาก
ๆ มาก
ๆ 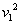 จะมีค่ามากกว่า จะมีค่ามากกว่า
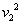 มาก
ๆ ดังนั้นสามารถตัด มาก
ๆ ดังนั้นสามารถตัด 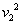 ในสมการข้างต้นทิ้งได้
จะได้ ในสมการข้างต้นทิ้งได้
จะได้
    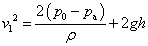
เราเรียกอัตราเร็วของน้ำ v1 ที่ไหลออกจากท่อว่า efflux
speed ซึ่งมีค่าขึ้นกับผลต่างความดัน 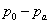 และความสูง
ถ้าด้านบนของถังเปิด และความสูง
ถ้าด้านบนของถังเปิด 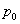 จะเท่ากับ จะเท่ากับ
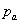 ทำให้ได้ ทำให้ได้
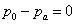 ในกรณีนี้จะได้ ในกรณีนี้จะได้
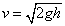 นี่คืออัตราเร็วของน้ำที่ไหลออกมาจากท่อ(รู)ข้างถังที่เปิดฝาอยู่
โดยที่ท่ออยู่ต่ำกว่าผิวน้ำภายในถังเป็นยะยะ h อัตราเร็วที่ได้นี้มีขนาดเท่ากับอัตราเร็วที่วัตถุตกอย่างอิสระในระยะความสูง
h ผลที่ได้สำหรับอัตราเร็วของน้ำที่ไหลออกจากรูข้างถังนี้เป็น ทฤษฎีของ
Torricelli นี่คืออัตราเร็วของน้ำที่ไหลออกมาจากท่อ(รู)ข้างถังที่เปิดฝาอยู่
โดยที่ท่ออยู่ต่ำกว่าผิวน้ำภายในถังเป็นยะยะ h อัตราเร็วที่ได้นี้มีขนาดเท่ากับอัตราเร็วที่วัตถุตกอย่างอิสระในระยะความสูง
h ผลที่ได้สำหรับอัตราเร็วของน้ำที่ไหลออกจากรูข้างถังนี้เป็น ทฤษฎีของ
Torricelli
UP
 |
|















