 ในตอนที่แล้ว เราได้พิจารณาพลังงานของระบบ
เมื่อมีเฉพาะแรงอนุรักษ์มากระทำ สำหรับในตอนนี้ จะพิจารณากรณีทั่วไป
คือมีทั้งแรงอนุรักษ์ และแรงไม่อนุรักษ์มากระทำภายในระบบ
ในตอนที่แล้ว เราได้พิจารณาพลังงานของระบบ
เมื่อมีเฉพาะแรงอนุรักษ์มากระทำ สำหรับในตอนนี้ จะพิจารณากรณีทั่วไป
คือมีทั้งแรงอนุรักษ์ และแรงไม่อนุรักษ์มากระทำภายในระบบ
 โดยอาศัยทฤษฎีบทงานและพลังงานจลน์
โดยอาศัยทฤษฎีบทงานและพลังงานจลน์

เมื่อ
W คืองานรวมทั้งหมดของระบบ ดังนั้นเมื่อมีทั้งแรงอนุรักษ์
และแรงไม่อนุรักษ์มากระทำต่อระบบ งานรวมทั้งหมด สามารถแบ่งออกได้เป็นสองส่วนคือ
งานเนื่องจากแรงอนุรักษ์

และแรงเนื่องจากแรงไม่อนุรักษ์
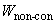
 เนื่องจากงานที่เกิดจากแรงอนุรักษ์
มีความสัมพันธ์ กับการเปลี่ยนแปลงพลังงานศักย ์ ตามสมการที่
(3-24)
เนื่องจากงานที่เกิดจากแรงอนุรักษ์
มีความสัมพันธ์ กับการเปลี่ยนแปลงพลังงานศักย ์ ตามสมการที่
(3-24)
 สมการที่
(3-33) เขียนใหม่ได้เป็น
สมการที่
(3-33) เขียนใหม่ได้เป็น
 สมการที่
(3-34) แสดงให้เห็นว่า พลังงานกลรวม (ทางขวามือของสมการ)
มีค่าเท่ากับ งานที่เกิดขึ้นเนื่องจากแรงไม่อนุรักษ์
และเมื่อแทนสมการที่ (3-30) และ (3-31) ลงในสมการที่
(3-34) จะได้สมการแสดงพลังงานของระบบเป็น
สมการที่
(3-34) แสดงให้เห็นว่า พลังงานกลรวม (ทางขวามือของสมการ)
มีค่าเท่ากับ งานที่เกิดขึ้นเนื่องจากแรงไม่อนุรักษ์
และเมื่อแทนสมการที่ (3-30) และ (3-31) ลงในสมการที่
(3-34) จะได้สมการแสดงพลังงานของระบบเป็น
 สำหรับระบบที่มีทั้งแรงอนุรักษ์
และแรงไม่อนุรักษ์มากระทำ พิจารณาได้จากตัวอย่างต่อไปนี้
สำหรับระบบที่มีทั้งแรงอนุรักษ์
และแรงไม่อนุรักษ์มากระทำ พิจารณาได้จากตัวอย่างต่อไปนี้
| |
 ตัวอย่างที่ 1-5
ตัวอย่างที่ 1-5 |
 |
จากรูปแสดงระบบซึ่งประกอบด้วยสปริง หนังสือ
และพื้นซึ่งมีความฝืด กำหนดให ้สปริงมีค่าคงตัว300
N/m วัตถุมีมวล1.60 kg และสัมประสิทธิ์ของแรงเสียดทาน
ระหว่างหนังสือกับพื้นมีค่า 0.22
ถ้าอัดกล่อง เข้ากับสปริงห่างจากตำแหน่งสมดุล
0.75 m ดังแสดงในรูป จงหา
(ก) ความเร็วของกล่อง เมื่อมันเคลื่อนที่ผ่านตำแหน่ง
ซึ่งอยู่ห่างจากจุดสมดุลของสปริงเป็นระยะทาง
1.50 m ดังรูป
(ข) จงหาตำแหน่งที่ไกลที่สุดที่กล่องเคลื่อนที่ไปถึง
วิธีทำ
(ก)
งานส่วนนี้กลายเป็นพลังงานจลน์
ที่เพิ่มขึ้นของวัตถ ุและเป็นงานที่ชดเชยงานเนื่องจากแรงเสียดทาน
เป็นความเร็วของกล่อง
เมื่อเคลื่อนที่ผ่านตำแหน่ง ซึ่งห่างจากจุดสมดุลของสปริงเป็นระยะทาง
1.50 m
วิธีทำ
(ข)
พลังงานจลน์ของกล่องที่หายไปจ
ะกลายเป็นงานที่ชดเชยงานเนื่องจากแรงเสียดทาน
นั่นคือ
หนังสือไปได้ไกลสุด = 22.3 + 1.5 = 23.8 วัดจากจุดสมดุล
|