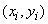
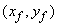
ถ้าเราทำการเลื่อนตำแหน่งของอนุภาคจากจุด ไปยังจุด ดังรูป ภายใต้แรงกระทำเนื่องจากความโน้มถ่วงของโลก

รูปที่ 3-7 แสดงเส้นทางการเคลื่อนที่ของอนุภาคจากจุด ไปยัง

เราสามารถหาการเปลี่ยนแปลงพลังงานศักย์ของอนุภาคนี้ได้โดยอาศัยสมการที่ (3-26) ภายใต้แรงกระทำเนื่องจากความโน้มถ่วงของโลก


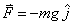
เมื่อพิจารณาระบบที่บริเวณใกล้ผิวโลก ค่า g คงที่

	(3-27)

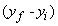
สมการที่ (3-27) แสดงให้เห็นว่า การเปลี่ยนแปลงของพลังงานศักย ์เนื่องจากความโน้มถ่วงของโลก ขึ้นอยู่กับการเปลี่ยนตำแหน่งของอนุภาคในแนวดิ่ง เท่านั้น

เมื่อพิจารณาสมการที่ 3-27 แล้วเขียนใหม่ในรูป

(3-27B)

จะได้ว่า เราสามารถที่จะกำหนดให้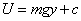

เพื่อให้ได้ 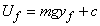และ 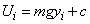นั่นคือ U ที่ตำแหน่งใดก็ขึ้นกับค่า y ที่ตำแหน่งนั้น เท่านั้น โดยที่ cเป็นค่าคงที่ของการอินทิเกรต และเราสามารถหาค่า (กำหนดค่า) c ได้ โดยการกำหนดจุดอ้างอิง เช่น กำหนดว่า U = 0 เมื่อ y = 0 เป็นต้น ซึ่งก็จะทำให้ได้สูตร

(3-27C)

หรือที่คุ้นเคยกันดีในรูป